Ensemble étudié par Henry Smith en 1875 et par Cantor en 1883. Georg Cantor (1845-1918) : mathématicien allemand. Autre nom : poussière de Cantor.

L'ensemble (triadique) de Cantor d'extrémité A et B est  l'attracteur des deux homothéties de rapport 1/3 et de centres A et B ; en général, on se place dans R avec A = 0 et B = 1 : C est l'attracteur dans  des deux homothéties : ,  .
Voici la suite des compacts  convergeant vers C en partant de [0, 1] :

intervalles fermés  où a est un naturel dont l'écriture en base 3 comporte au maximum n chiffres égaux à 0 ou 2 ; par exemple .

C est donc aussi l'ensemble des réels de [0, 1] ayant un développement en base 3 ne comportant que des 0 ou des 2 (remarquer qu’en base 3, les homothéties ci-dessus s’écrivent  et ).
C est un ensemble ayant la puissance du continu, compact, sans point isolé, d'intérieur vide, totalement discontinu et négligeable.
Sa dimension fractale est .

2C est l'ensemble unité associé à 1/3.

A l'instar de Mickey, l'ensemble de Cantor est à l'origine de très nombreux "produits dérivés" :
    - Le peigne de Cantor (qui est en fait de hauteur infinie), illustrant la construction de l'ensemble de Cantor.

    - Le triangle de Cantor
 

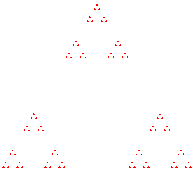C'est l'attracteur de 4 homothéties de rapport 1/3 centrées au sommet d'un triangle équilatéral ; sa dimension fractale est égale à 1.

    - Le carré de Cantor égal à C² :
 

C'est l'attracteur des quatre homothéties de rapport 1/3 centrées aux 4 sommets d'un carré ; sa dimension fractale est .

Une organisation humanitaire bien connue lui préférera certainement son complémentaire :

    - Le cube de Cantor C³ :
 

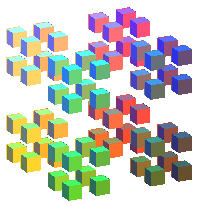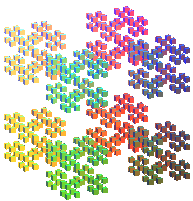C'est l'attracteur des huit homothéties de rapport 1/3 centrées aux 8 sommets du cube ; sa dimension fractale est  (inférieure à celle d'une surface !) ; il a été utilisé pour modéliser les galaxies.
    - Le tartan de Cantor, égal à  :
 

L'ensemble de Cantor présentant la particularité que l'ensemble des différences positives de ses éléments est égal à [0, 1] entier, la frontière de tout rectangle de dimensions  1 peut être recouverte par le tartan de Cantor, qui est pourtant négligeable.

Les intersections entre les lignes verticales et horizontales forment le carré de Cantor.
 

    - Le tipi de Cantor formé des segments joignant C à (1/2, 1)  (dénommés ci-dessous les "rayons"):
  Le tipi de Cantor est connexe (par arcs) mais si on lui ôte son sommet, l'ensemble obtenu possède une infinité de composantes connexes.
Plus fort : si on ne conserve dans le tipi de Cantor que les points dont l'ordonnée est rationnelle si la base du rayon passant par le point est ternaire, et les points dont l'ordonnée est irrationnelle si la base du rayon n'est pas ternaire, on obtient un ensemble qui est encore connexe, mais qui est tel que si on lui ôte un point (le sommet), l'ensemble obtenu est totalement discontinu : voir ici.
    - Les anneaux de Cantor (ou cible de Cantor), obtenus en faisant tourner l'ensemble de Cantor autour de son centre, permettant de modéliser les anneaux de Saturne :
 

    - Les rideaux de Cantor, visualisant la bijection existant entre C et [0, 1] (qui à tout élément ne s'écrivant qu'avec des 0 ou des 2 en base 3 fait correspondre le nombre obtenu en remplaçant les "2" par des "1", lu en base 2).
 

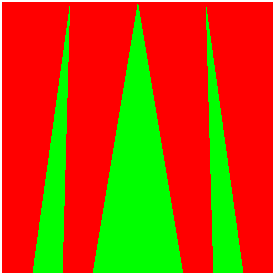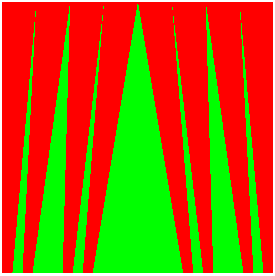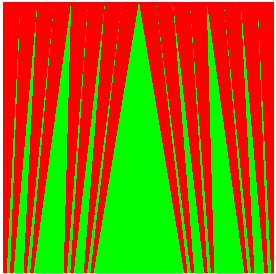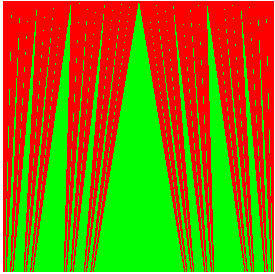
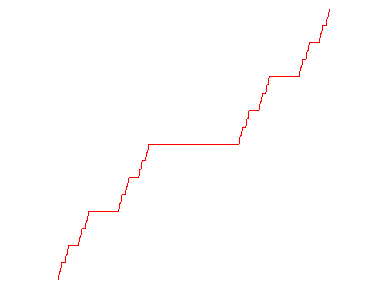
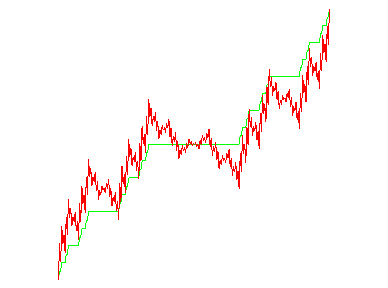
    - L'escalier de Cantor-lebesgue et son produit dérivé la courbe de Lebesgue :

En vert, l'escalier du diable, pour comparaison.

- Le tapis de Sierpinski, dont l'intersection avec une médiane ou une diagonale est l'ensemble de Cantor :

    - La courbe de Koch, dont la base est l'ensemble de Cantor.

La ville et le château de Cantor ...

fractal suivant

fractal précédent

courbes 2D

courbes 3D

surfaces

fractals

polyèdres

© Robert FERRÉOL 2001