.
| next surface | previous surface | 2D curves | 3DÂ curves | surfaces | fractals | polyhedra |
ROTATION SURFACE WITH CONSTANT GAUSSIAN CURVATURE
| Darboux
studied in 1890 the general surfaces with constant Gaussian
curvature.
This study comes from [Gray] page 473; see also [Valiron] page 467. |
The definition of the surface studied here is stated in its name.
First case: positive Gaussian curvature, equal to .
Polar parametrization:  .
First fundamental quadratic form:  .
Meridian radius of curvature:  ,
parallel radius of curvature:  .
Gaussian curvature:  ,
mean curvature:  . |
 |
 |
 |
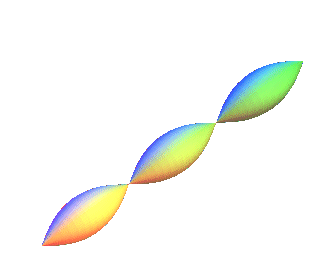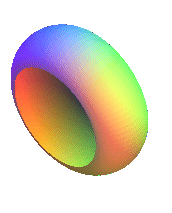| View of the case 0 < k < 1 | View of the case k = 1, that gives the sphere | View of the case k > 1 |
Remark: all the surfaces here are applicable to the sphere.
Second case: negative total curvature, equal to 
.
We also find 3 kinds of surfaces, but this time with three different parametrizations.
First kind: surface with a conical point:
Polar parametrization:  ,
0 < k < 1.
First fundamental quadratic form: .
Meridian radius of curvature:  ,
parallel radius of curvature:  .
Gaussian curvature:  ,
mean curvature:  . |
 |
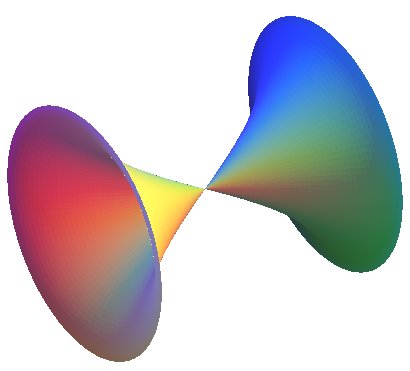Second type: surface that looks like a hyperboloid:
Polar parametrization:  ,
for any value of k.
First fundamental quadratic form: .
Meridian radius of curvature:  ,
parallel radius of curvature:  .
Gaussian curvature: ,
mean curvature: . |
 |
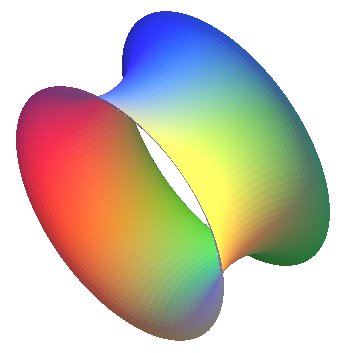The third type is that of the pseudosphere to which the previous surfaces are applicable.
REMARK 1: since the meridian radius of curvature of a
surface of revolution is that of the profile of the surface, and the parallel
radius of curvature is the length of the segment line MN joining
the point M on the surface to the intersection point N between
the normal and the axis, the profiles of the surfaces studied here are
none other than the curves for which the curvature is proportional to the
normal (or, which is equivalent, such that the product MI . MN
is constant, I being the center of curvature).
Compare to the elastic
curves.
REMARK 2: since the principal curvatures of a surface
of revolution with a profile parametrized by the curvilinear abscissa: 
are 
and 
,
the equation of the profiles studied here is the very classic equation: 
.
Compare these surfaces to the surfaces
with constant mean curvature, or Delaunay surfaces.
| next surface | previous surface | 2D curves | 3DÂ curves | surfaces | fractals | polyhedra |
© Robert FERRÉOL 2017