Rosace rhombique

ROSACE RHOMBIQUE
Rhombic rose, Rhombenrose

cas n = 20

Autre nom : rosette.
Site : schoengeometry.com/b-fintil.html

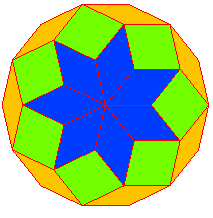
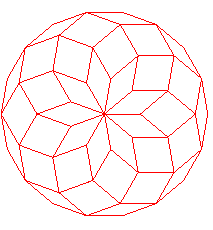
La rosace rhombique d'ordre n est la figure obtenue en partant de n losanges identiques et jointifs, complétée par des anneaux concentriques de losanges jusqu'à ce que la figure devienne convexe.

Les premiers losanges ont pour angles et son supplémentaire, la série suivante : et son suppplémentaire, puis etc.

Pour n pair on obtient donc anneaux de n losanges identiques d'où un pavage du polygone régulier à n côtés par losanges.

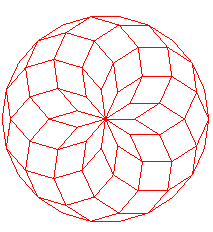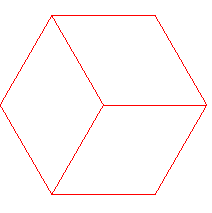
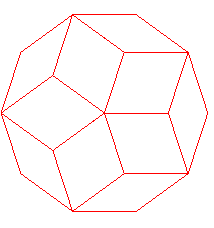
Pour n impair on obtient anneaux de n losanges identiques d'où un pavage du polygone régulier à 2n côtés par losanges.


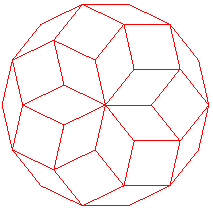
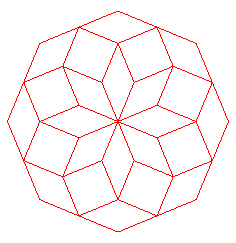
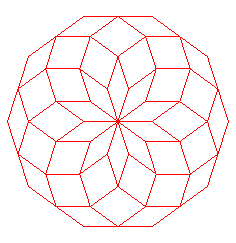
n = 3	n = 5 Les deux types de losanges sont célèbres car constitutifs des pavages de Penrose (angles 36° et 72°).	n = 7	n = 9	n = 11

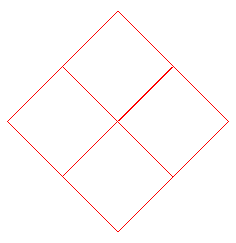
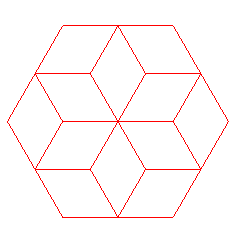
n = 4	n = 6	n = 8	n = 10	n = 12

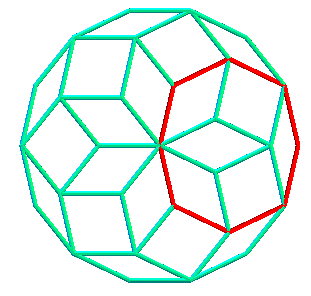
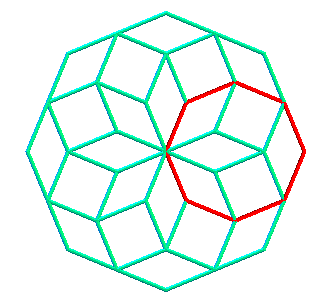
Dans le cas n pair, la rosace rhombique est aussi obtenue en faisant tourner n fois d'un n-ième de tour autour de l'un de ses sommets un polygone régulier à n côtés, de dimension moitié du polygone extérieur. Chaque petit polygone est alors pavé par

losanges (voir à zonogone).

Dans le cas n impair, on obtient aussi la figure par rotations successives d'un polygone à côtés égaux, mais non régulier.
Plus précisément ce polygone est un n+1-zonogone équilatéral, ayant 2 angles opposés égaux à (l'un au centre de rotation ) et les n-1 autres angles égaux à .

Pour n grand (cf. figure d'entrée), la figure tend à se confondre avec la rosace classique obtenue en faisant tourner un cercle au lieu d'un polygone.

Assiette marocaine décorée en rosace rhombique (n = 30)

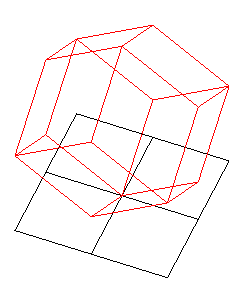
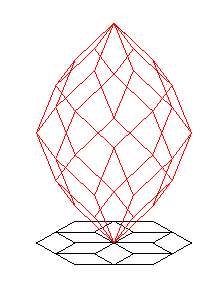
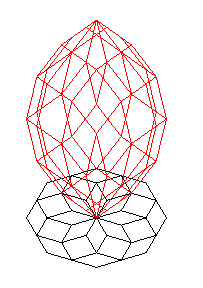
Si l'on élève au dessus de chaque polygone 2 lignes polygonales de pente constante (dont les sommets sont sur une hélice circulaire), on obtient, un élégant polyèdre rhombique, appelé rhombizonoèdre polaire, à n(n – 1) faces.

n = 4 : le polyèdre n'est autre que le dodécaèdre rhombique	n = 6	n = 8	n = 12

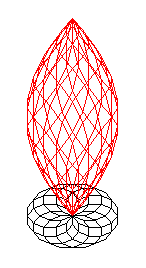Quand n tend vers l'infini, ce polyèdre tend vers une portion de la surface nommée dans ce site "révolution de la sinusoïde", obtenue en faisant tourner une 1/2-arche de sinusoïde autour de sa base.

Rhombizonoèdre polaire, par Alain Esculier.

polyèdre suivant polyèdre précédent courbes 2D courbes 3D surfaces fractals polyèdres