CATÉNOÏDE GAUCHE, SURFACE MINIMALE DE RIEMANN
Skew
catenoid, Riemann's minimal surface, schiefes Katenoid,
riemannsche minimale Fläche
| surface suivante | surface précédente | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
CATÉNOÏDE GAUCHE, SURFACE MINIMALE DE RIEMANN
Skew
catenoid, Riemann's minimal surface, schiefes Katenoid,
riemannsche minimale Fläche
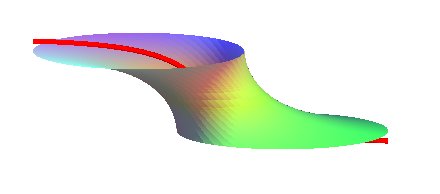
| Surface étudiée par Riemann en 1860, Enneper
en 1869.
Bernhard Riemann (1826 - 1866) mathématicien allemand. Ref : [NITSCHE] p. 84. |
Paramétrisation cartésienne : 
(donnant pour u 
1, la partie située dans le demi-espace z
0).
Cercles horizontaux de rayon u centrés en  (courbe
rouge ci-dessus).
Nota : les intégrales ci-dessus se calculent à l'aide des fonctions elliptiques. |
Le caténoïde gauche d'équation
donnée ci-dessus est la solution au problème de recherche
des
surfaces minimales cerclées.
Notons que les cercles sont donc forcément parallèles entre
eux, et la ligne des centres située dans un plan perpendiculaire
à ceux des cercles.
Le caténoïde gauche fournit donc aussi une
solution au problème de Plateau consistant à trouver une
surface minimale joignant deux cercles situés dans des plans parallèles
(mais notons qu'il y a des conditions sur les deux cercles pour que la
surface existe - voir déjà le cas des cercles coaxiaux à
caténoide).
Si on fait k = 0 dans les formules ci-dessus, on
retrouve le caténoïde droit classique.
La surface est située entre les deux plans 
et est asymptote à ces deux plans
(  ).
Par des translations du motif précédent et en ajustant les demi-plans asymptotes, on obtient une surface minimale lisse périodique, applée surface minimale de Riemann. Toutes les sections par des plans horizontaux sont des cercles ou des droites. |
|
Voir aussi la surface minimale
de Riemann finie.
| surface suivante | surface précédente | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
© Robert FERRÉOL 2018
