Paramétrisation de Weierstrass :
Première forme quadratique fondamentale pour le
cas :
.
| surface suivante | surface précédente | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
SURFACE MINIMALE
Minimal
surface, MinimalFläche
| Surfaces étudiées par Lagrange en 1760,
Meusnier en 1776, Monge en 1784, Legendre en 1787, Scherk en 1835, Weierstrass
en 1866 etc...
Autres noms : élassoïde (nom donné par Ribaucour en 1880 [Etude sur les élassoïdes ou surfaces à courbure moyenne nulle]), surface optimale. Sites : Wikipedia Classical Minimal Surfaces in Euclidean Space by Examples Diaporama avec de nombreux exemples Cours de Meeks et Perez virtualmathmuseum.org/Surface/gallery_m.html www.ugr.es |
| Équation aux dérivées partielles
: Paramétrisation de Weierstrass : Première forme quadratique fondamentale pour le
cas |
.Une surface minimale est une surface dont chaque point possède un voisinage qui est une surface d'aire minimale parmi les surfaces de même bord que celui de ce voisinage. Une condition nécessaire et suffisante est que la courbure moyenne en tout point soit nulle, autrement dit que les deux rayons de courbure principaux soient opposés en tout point, ou encore que l'indicatrice de Dupin soit une hyperbole équilatère ; excepté dans le cas du plan, ses points sont donc tous hyperboliques ; les lignes asymptotiques forment un double réseau de courbes orthogonales, et les lignes de courbures sont leurs bisectrices.
Cette condition de courbure moyenne nulle signifie que l'énergie de courbure est nulle et donc que la stabilité de ces surfaces est maximale ; elle est réalisée physiquement par tout film de savon soumis à des pressions égales de chaque côté (lorsque les pressions diffèrent, on obtient des surfaces à courbure moyenne constante).
Toute surface d'aire minimale s'appuyant sur une ou plusieurs courbes bornées est minimale au sens ci-dessus. La réciproque en est fausse : par exemple, une portion d'hélicoïde droit entre deux segments de droites parallèles est une surface minimale mais d'aire supérieure à celle d'une portion de plan.
Le théorème de Plateau (de Joseph Plateau (1801 - 1883) : physicien belge, mais le théorème n'a été démontré qu'en 1931 par Douglas et Rado) affirme qu'il existe toujours une surface minimale dont le bord est un contour fermé borné sans auto-intersection et non noué donné (et cette surface plus son bord est homéomorphe à un disque plus son bord) ; de plus ces surfaces sont en nombre fini, ne se recoupent pas, et l'une d'entre elle est une surface d'aire minimale parmi toutes les surfaces s'appuyant sur ce contour.
Le théorème de Björling affirme, lui, qu'il existe une surface minimale analytique ayant pour géodésique une courbe donnée (cette surface étant unique si l'on impose la valeur du vecteur normal le long de la courbe).
La ligne droite est le plus court chemin d'un point à
un autre, mais on verra que, par contre, une surface formée de lignes
droites (i. e. réglée)
est rarement minimale...
| Exemples | Paramétrisation de Weierstrass |
| - le caténoïde (1740), seule surface de révolution non plane qui soit minimale, surface de Björling associée à un cercle | |
| - líhélicoïde droit (1776) seule surface réglée non plane qui soit minimale | |
| - les hélicoïdes minimaux (1835) comprenant les deux précédentes, surfaces de Björling associées à une hélice circulaire | |
| - les surfaces de Scherk (1835), la première étant la seule surface de translation qui soit minimale | |
| - la surface minimale de Catalan (1855), surface de Björling associée à une cycloïde | |
| - la surface d'Henneberg (1858), surface de Björling associée à une parabole cubique | |
| - la surface de Bour (1861) | |
| - la surface d'Enneper (1863), surface de Björling associée à une cubique de Tschirnhausen et surface de Plateau associée à une couture de balle de tennis | |
| - la famille des surfaces d'Enneper englobant les 2 précédentes | |
| - la fleur de Jeener | |
| - la famille des surfaces de Richmond | |
| - le caténoïde gauche ou surface minimale de Riemann, seule surface cerclée minimale (1860) | fonctions elliptiques |
| - la surface minimale de Riemann finie (198..) | |
| - le ruban de Möbius minimal de Meeks (1981) | |
| - la surface de Costa (1982) | |
| - le trinoïde et les n-noïdes (1983) | |
| - les surfaces minimales tripériodiques :
surfaces de Schwarz (1864), surface de Neovius (1883), gyroïde (1970) |
| Si l'on prend La vue de droite montre les lignes de coordonnées ; les projections sur un plan horizontal des lignes à u constant sont des trochoïdes. |
 |
 |
| Si l'on prend |
|
 |
 |
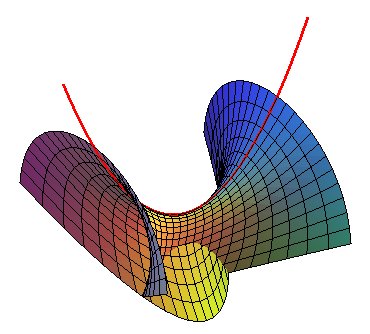
Surface de Björling associée à une lemniscate
de
|
| surface suivante | surface précédente | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
© Robert FERRÉOL 2014