Duporcq curve

ORTHOGONAL PURSUIT CURVE, DUPORCQ CURVE

Curve studied by Duporcq and Mannheim in 1902, Balitran in 1914, Egan in 1919, Masurel in 2014.
Ernest Duporcq (1873-1903): French mathematician.
Other name: crab curve.
See also: Walter Wunderlich, Über die Hundekurven mit konstantem Schielwinkel, Monatshefte für Mathematik, 1957, Volume 61, Issue 4, pp 299-303.

Differential system: , yielding, when , , i.e. .

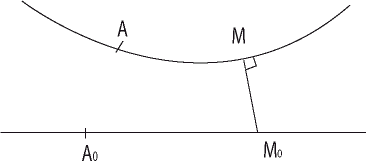
The orthogonal pursuit curves are the trajectories of a point M the motion of which is always in a direction perpendicular to that of the other moving point M₀ (the pursuee), the two moving points having proportional speeds .
Given the trajectory of M₀, the trajectory of M is therefore defined in this case by the fact that (MM₀ ) is perpendicular at M to its trajectory, and the curvilinear abscissa of M is proportional to that of M₀: .
One can imagine a crab at M always walking face to face with the pursuee M₀ and these curves could be called "(pursuit) curves of the crab".

I) In the case where M₀ has a linear movement, the trajectories of the "pursuer" are called "Duporcq curves".
Egan proved that the vector then has the same movement as a body in Newtonian attraction, and therefore describes a conic with eccentricity e (hence the choice of the letter e for the ratio between the speeds, instead of the more classic k).

First case: , elliptic case.

Cartesian parametrization: , , .
Curvilinear abscissa: .

Opposite, in blue, the elliptic movement of the vector is indicated.
The Duporcq curve is, in this case, the image by a scaling in one direction with ratio of an elongated cycloid with ratio .
NOTA 1: it is the only scaling that allows to integrate the curvilinear abscissa thanks to elementary functions.
NOTA 2: in the formulas above, and as it can be noticed in the animation opposite, the speeds of M and M₀ are proportional, but not constant.

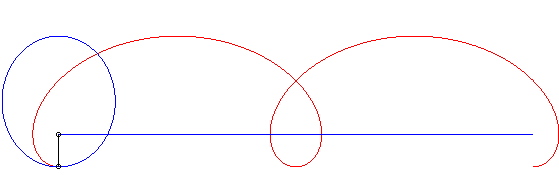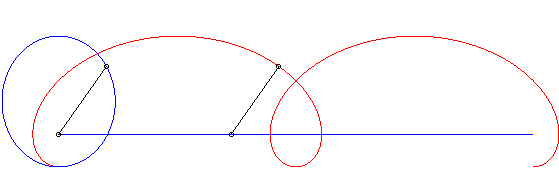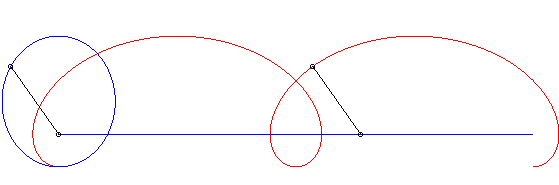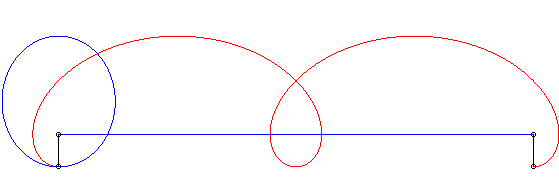Second case: , parabolic case.
a) the pursuer and the pursuee have, at a given time, their speeds in the same direction: the pursuer evidently follows a line parallel to that followed by the pursuee.

b) the pursuer and the pursuee have, at a given time, their speeds in opposite directions.

Cartesian parametrization: ,,
Curvilinear abscissa: .

Opposite, in blue, the parabolic movement of the vector is indicated.
The Duporcq curve is none other, in this case, than the Tschirnhausen cubic.
NOTA: the movement of M is the composition of a parabolic motion and a translation.

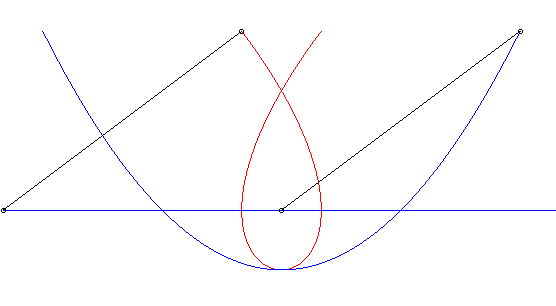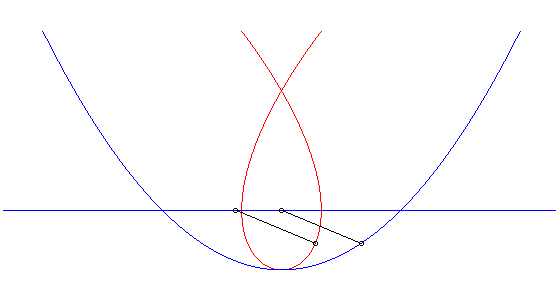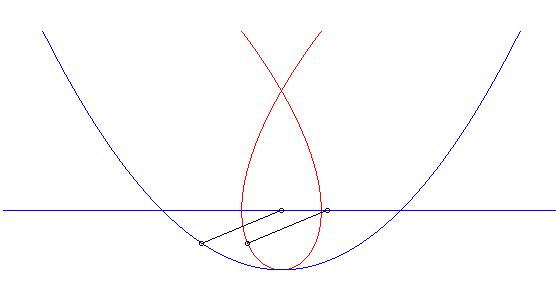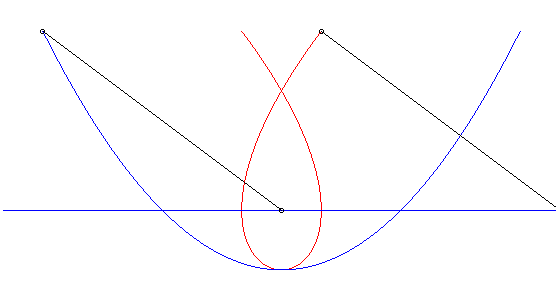Third case: , hyperbolic case.

a) the pursuer and the pursuee are at the same point at a given time: they follow to secant lines.

This case is excluded in the following.

b) The pursuer and the pursuee have, at a given time, their speed in the same direction:

Cartesian parametrization:, ,

Curvilinear abscissa: .
Opposite, in blue, the hyperbolic movement of the vector is indicated.

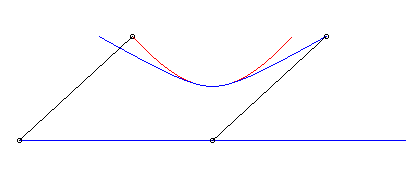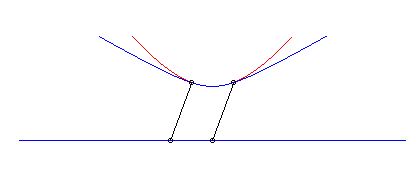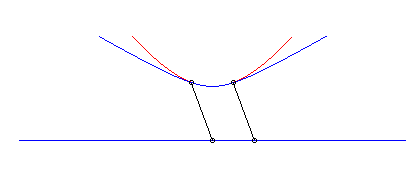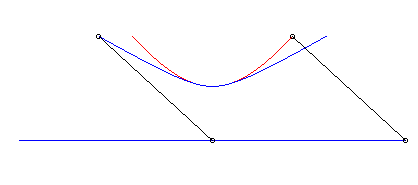c) the pursuer and the pursuee have, at a given time, their speeds in opposite directions:

Cartesian parametrization: , , .
Curvilinear abscissa: .
Opposite, in blue, the hyperbolic movement of the vector is indicated.

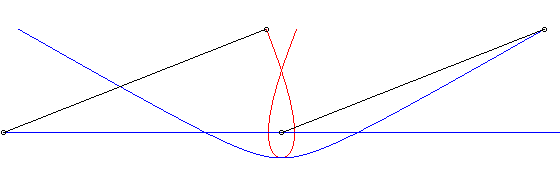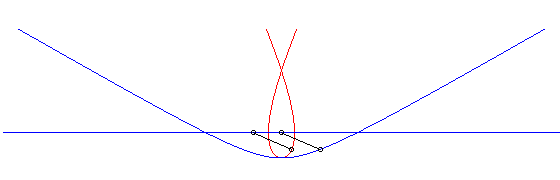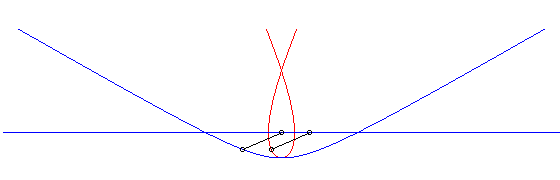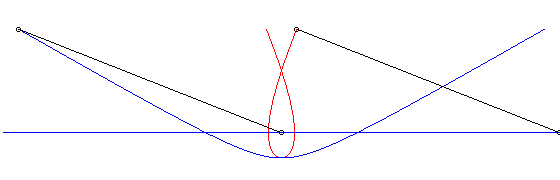REMARK: Mannheim proved that the Duporcq curve with parameter e is the roulette with linear base of the pole of the Sturm spiral satisfying .

II) Case where the pursuee describes any curve:

Vectorial differential equation: 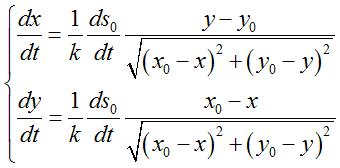, that translates into the differential system:
( = pursuee, = pursuer, ).

For a pursuee on the circle with centre O and radius R, we get the differential system: which enables to draw the curves thanks to a software.

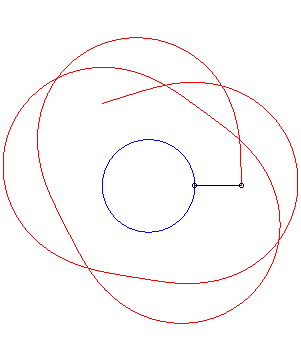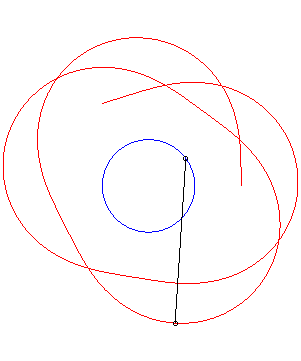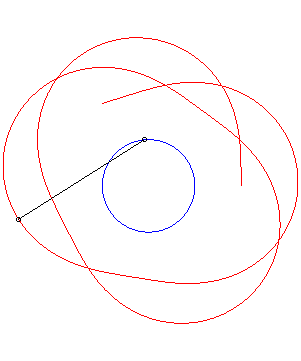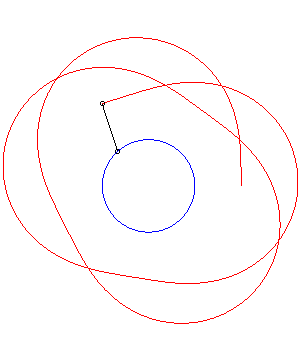
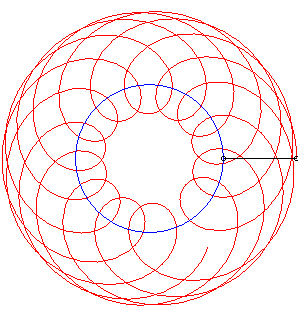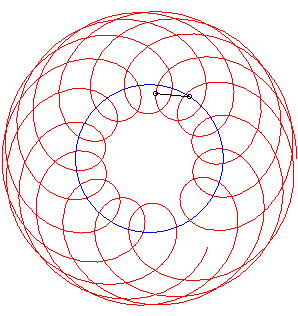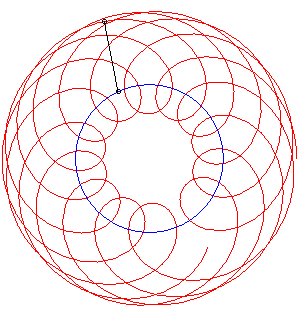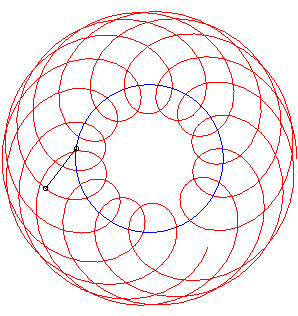
An example with k = 1.
An example with k = 1/3. The shadowing curve associated to the point describing a circle (in blue below) and to a point on the circle (the tree) provides a circular special case of the curve of the pursuer associated to a circle.
If is the radius of the pursuee's circle and R that of the pursuer's circle, we have .
Below, an example with k = 1/2, .

VARIATION (based on an idea of Alain Esculier): the speed of the pursuer is no longer proportional to that of the pursuee, but to its distance from it.

Vectorial differential equation: , which translates into the linear differential system: .
Equations of the movement of the pursuer: .

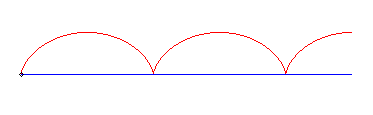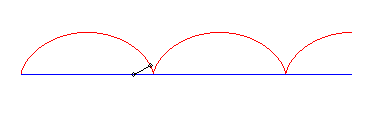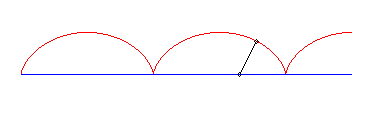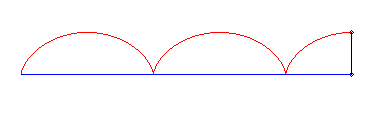
I) Linear pursuee.

For a pursuee (vt, 0), equations of the movement of the pursuer passing by (0, b):
(a = v/k).
Therefore, it is a trochoid with ratio , which is a cycloid if .

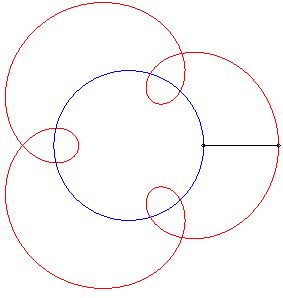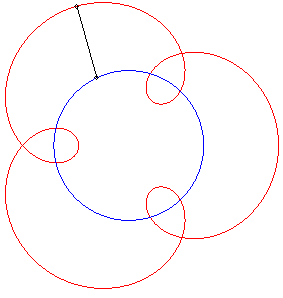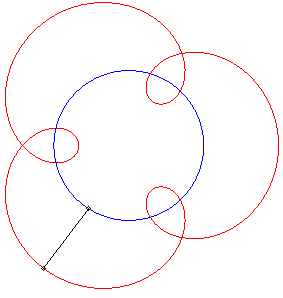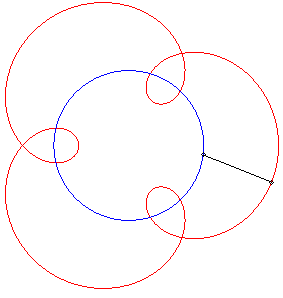
II) Circular pursuee.

For a pursuee , equations of the movement of the pursuer passing by (0, a) when :
. It is an epitrochoid when and a hypotrochoid when , epicycloid and hypocycloid when a = R. The parameter q is equal to .

When , we get: , which is none other than an involute of a circle (more precisely, involute of the circle described by the pursuee).

next curve previous curve 2D curves 3D curves surfaces fractals polyhedra

An example with k = 1.	An example with k = 1/3.	The shadowing curve associated to the point describing a circle (in blue below) and to a point on the circle (the tree) provides a circular special case of the curve of the pursuer associated to a circle. If is the radius of the pursuee's circle and R that of the pursuer's circle, we have . Below, an example with k = 1/2, .

For a pursuee , equations of the movement of the pursuer passing by (0, a) when : . It is an epitrochoid when and a hypotrochoid when , epicycloid and hypocycloid when a = R. The parameter q is equal to .
When , we get: , which is none other than an involute of a circle (more precisely, involute of the circle described by the pursuee).