next curve previous curve 2D curves 3D curves surfaces fractals polyhedra

CYLINDROCONICAL CURVE

Cylindroconical curves are the intersections between a cylinder of revolution and a cone of revolution. Therefore, they are biquadratics.
 
In the case of a cylinder with radius a the axis of which is perpendicular to that of a cone with half-angle at the vertex equal to 2α:
System of Cartesian equations:  where  and d is the distance from the vertex of the cone to the axis of the cylinder.
Cartesian parametrization: .

 

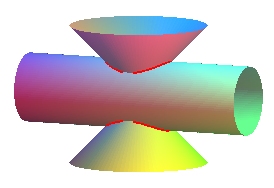
d = 0


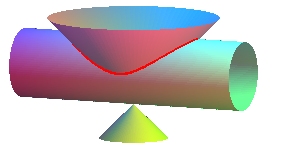
Here, d = a: the vertex of the cone is an isolated point of the curve.

 
: reunion of two ellipses.


 
 
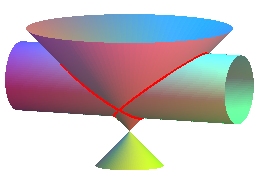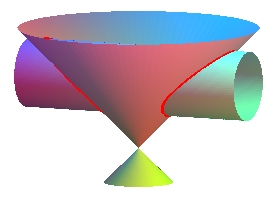
In the case of a cylinder with radius a the axis of which is parallel to that of a cone with half-angle at the vertex equal to 2α:
System of Cartesian equations:  where  and d is the distance from the vertex of the cone to the axis of the cylinder.
Cartesian parametrization: .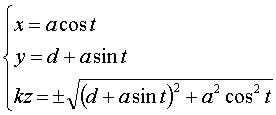

 

d = 0: two circles.

0 < d < a

d = a: Viviani curve.

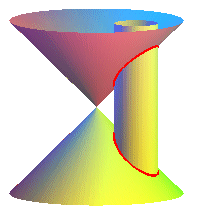
d > a

Naturally, there are a lot of different cases.


Image sent by Julien Vorpe


next curve previous curve 2D curves 3D curves surfaces fractals polyhedra

© Robert FERRÉOL  2018