Notion introduite en 1897 par Fricke et Klein. Voir aussi : CircInvFrac/InvLimSet/InvLimSet.html www.josleys.com/articles/JosLeyDelahayeV2.pdf images.math.cnrs.fr/Les-ensembles-limites-de-groupes.html Audibert, géométrie des pavages p. 313 à 319.

Étant donnée une famille d'inversions du plan de disques d'inversion 2 à 2 disjoints ou tangents extérieurement, il existe un unique compact non vide inclus dans la réunion des disques fermés et globalement invariant par chacune de ces inversions, appelé l'ensemble limite associé à ces inversions.
La notion est similaire à celle d'attracteur d'une famille de contractions, en plus complexe car les inversions ne sont des contractions que si on les restreint à l'extérieur du disque d'inversion.

Si les n inversions sont associées à des disques ouverts D1,..., Dn  et si on part d'un compact K du plan inclus dans la réunion des disques fermés, on obtient une contraction en transformant K  en K1 union ... union Kn  où Ki est l'image par l'inversion fi  de K privé de Di .
En réitérant le procédé, on obtient une suite de compacts convergeant pour la métrique de Hausdorff vers l'ensemble limite.

Dans les exemples ci-dessous, on remarquera bien que l'inverse de la partie de l'ensemble limite incluse dans un des disques d'inversion par le bord de ce disque donne le reste de l'ensemble limite.
 

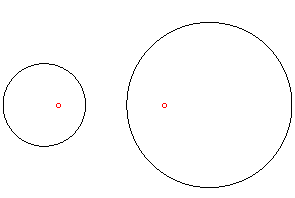
Pour deux inversions, l'ensemble limite est constitué des deux points limites du faisceau de cercles engendré par les deux cercles d'inversion.
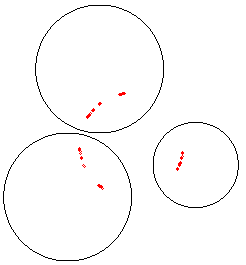
Pour trois inversions, l'ensemble limite est un ensemble du type Cantor inclus dans le cercle (ou la droite) orthogonal(e) aux trois cercles d'inversion (lequel est globalement invariant par chacune des inversions). Lorsque les trois cercles sont tangents, on obtient le cercle orthogonal entier. La figure, et les suivantes ont été obtenues par l'algorithme probabiliste consistant, partant d'un point quelconque, à tirer au hasard une des 3 inversions, à déterminer son image par cette inversion et à réitérer le procédé. La suite obtenue est affichée à partir du 10ème terme.
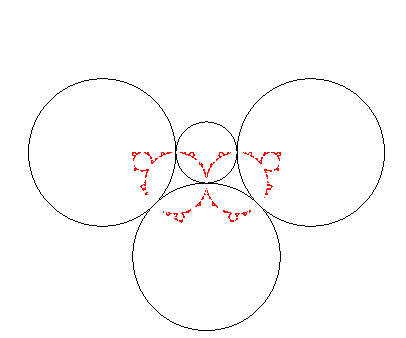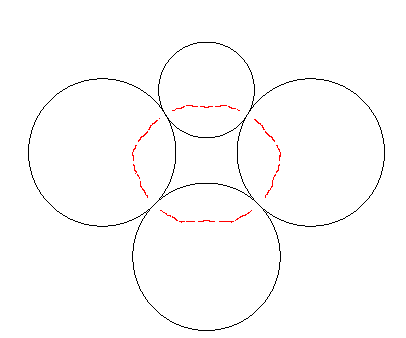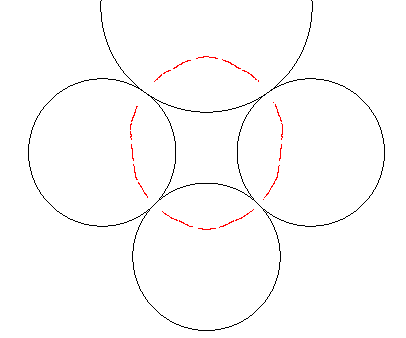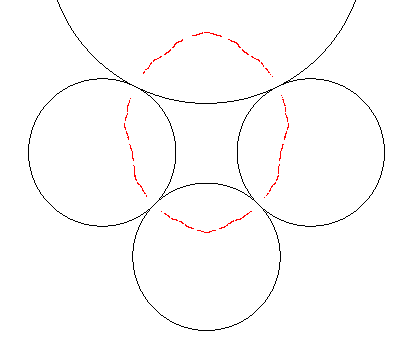
A partir de 4 inversions, on obtient un fractal plus complexe, qui est connexe si chaque cercle d'inversion en touche deux autres au moins ; s'il existe un cercle orthogonal à tous les cercles de départ, l'ensemble limite est inclus dans ce cercle.
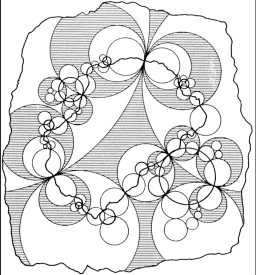
La figure ci-contre est la figure originale tracée par un élève de Robert Fricke, partant des 5 grands cercles blancs. Cette figure est importante historiquement car c'est la première apparition (en 1897) d'un objet fractal, avant le flocon de Koch (1905). Voir plus de détails dans cet article de Michèle Audin et Arnaud Chéritat, rendant hommage à l'anonyme dessinateur du premier fractal.
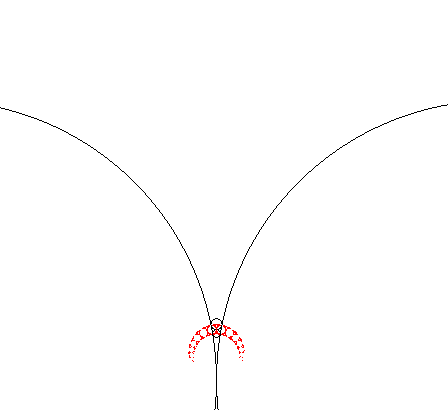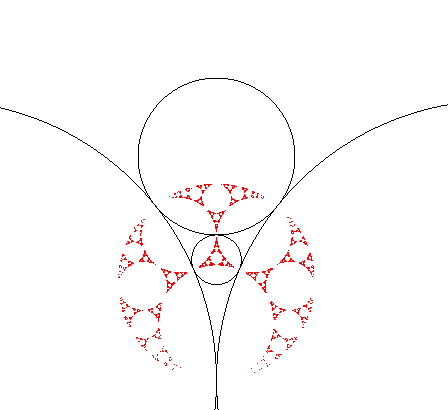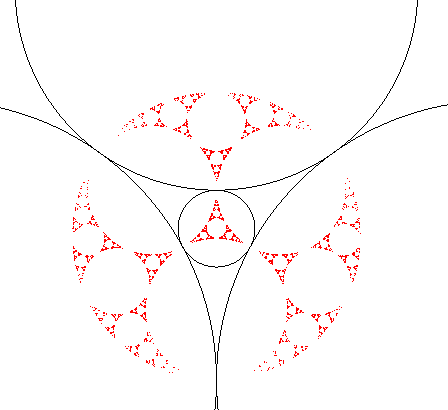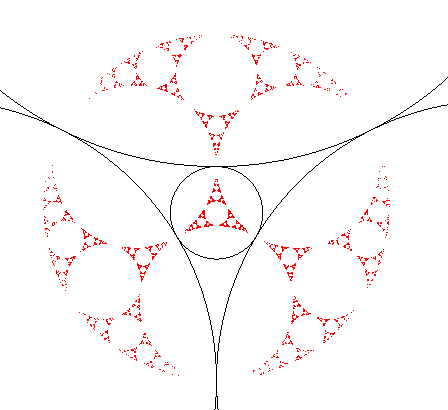
Lorsque 3 des cercles d'inversion sont 2 à 2 tangents, l'ensemble limite contient le cercle orthogonal à ces 3 cercles (passant par les 3 points de tangence). L'ensemble limite associé à 4 cercles d'inversion deux à deux tangents n'est donc autre que la baderne d'Apollonius (du deuxième type) construite à partir des 4 cercles orthogonaux à 3 de ces cercles !
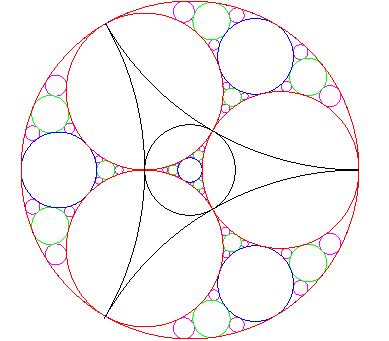
Voici donc comment on peut construire la baderne par inversions : partir des 4 cercles rouges ; chacun étant invariant par 3 des 4 inversions associées aux cercles noirs, la première étape donne les 4 cercles bleus ; la deuxième donne les 4.3= 12 cercles verts, la troisième, les 4.3²=36 cercles roses, et il faudrait continuer à l'infini. Comparer avec la construction de la baderne par cercles tangents successifs. Voir sur deux pages d'Alain Esculier comment on peut construire d'autres ensembles limites similaires, par images de cercles par des inversions :   - cercles et sphères d'Apollonius  - badernes sphériques	-
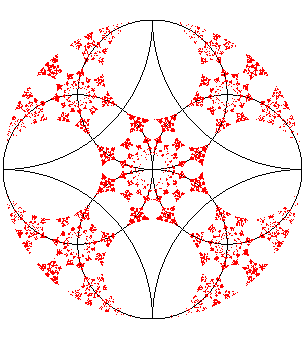
Ci-contre, exemple d'ensemble limite associé à 8 cercles dont certains se croisent orthogonalement :
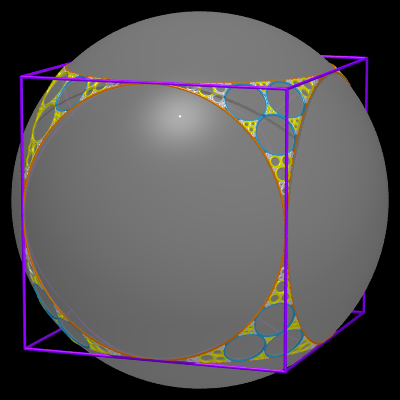
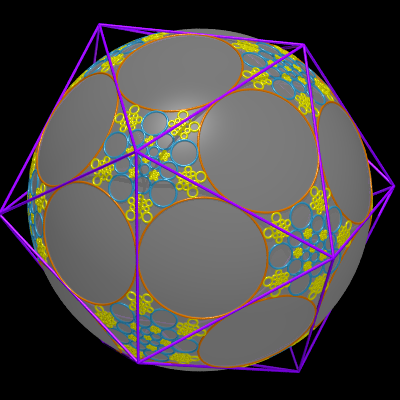
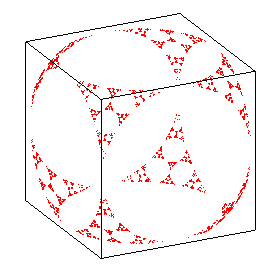
La notion se généralise à l'espace. Ci-contre, vue de l'ensemble limite associé à 8 sphères d'inversions centrées aux sommets d'un cube, de rayon la demi-arête du cube. L'ensemble limite est inclus dans la sphère inscrite dans les arêtes du cube (sphère globalement invariante par chacune des inversions) et les calottes sphériques de frontières les cercles de l'ensemble limite constituent un empilement complet de cette sphère.

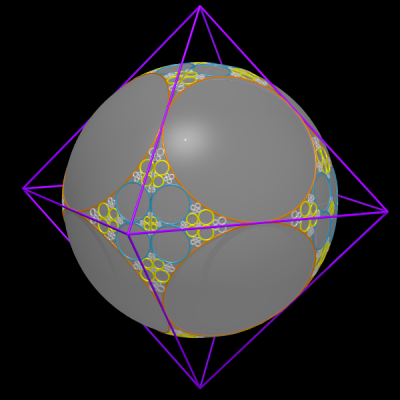
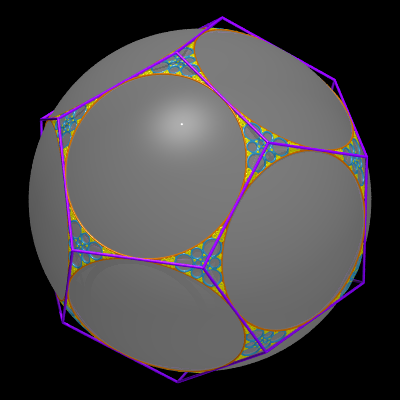
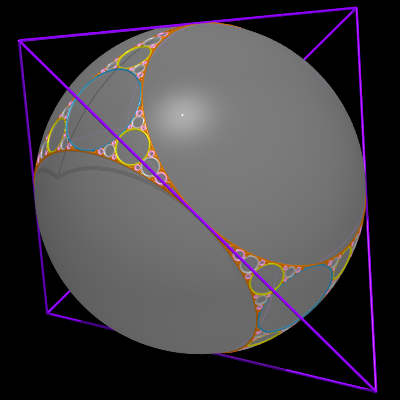
Voici, réalisés avec povray par Alain Esculier, les ensembles limites associés aux sphères d'inversion centrées aux sommets des polyèdres réguliers, de rayon la demi-arête.

Cube	Voici comment cet ensemble limite est construit (S est le nombre de sommets du polyèdre, F le nombre de faces, D le degré de chaque sommet, O l'ordre de chaque face, S.D = F.O) :  les F cercles oranges inscrits dans chaque face sont transformés par les S–O inversions qui ne les laissent pas invariants en F.(S–O)=S.(F–D) cercles bleus ; chaque D-gone curviligne associé à chaque sommet possède donc F–D cercles bleus. Les cercles bleus sont transformés en les S².(F–D) cercles jaunes, ceci étant répété normalement à l'infini, mais les cercles blancs ou roses de l'étape suivante n'ont été tracés que pour le cube, l'octaèdre et le tétraèdre.	Octaèdre
Dodécaèdre	Tétraèdre  Par projection stéréographique, on obtient  une baderne d'Apollonius du deuxième type	Icosaèdre

 

fractal suivant

fractal précédent

courbes 2D

courbes 3D

surfaces

fractals

polyèdres

© Robert FERRÉOL  2014