where
1) 
with g positive, C1
on ]a, b[,
2) 
concave on [a, b] .
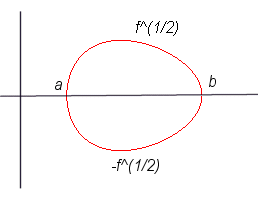
Profile of the corresponding egg, curve y²=f(x).
| next surface | previous surface | 2D curves | 3D curves | surfaces | fractals | polyhedra |
OVOID
| Other name: ovaloid.
YouTube video on finding the equation of a bird's egg profile : www.numberphile.com/videos/the-ultimate-egg-quation Paper : scienceline.org/2021/11/a-new-equation-can-describe-every-egg/ |
An ovoid is a surface shaped like an egg.
In a general fashion, we can give the following definition:
surface of class C1,
boundary of a bounded convex subset of space. Then, a closed surface of
class C1 all
the points of which are elliptic
is an ovoid.
To come closer to an egg, we can give the following definition:
| Cylindrical equation:
where
1) 2) |
Profile of the corresponding egg, curve y²=f(x). |
Examples:
the ellipsoid
of revolution ( ,
k being the flattening of the ellipse), opposite with k = 3/4 |
 |
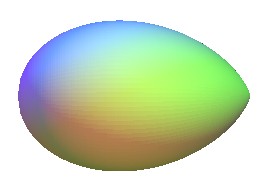
the Kepler
ovoid, the profile of which is a simple folium ( ,
a = 0, b = 1) |
 |
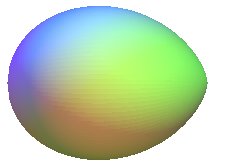
the ovoid with profile half a double
egg ( ,
a = 0, b = 1) |
 |
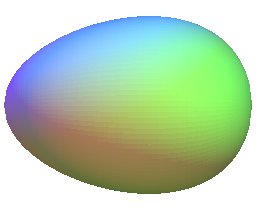
the ovoid with profile the oval of the cubical
hyperbola with an oval, or Hügelschäffer
egg ( ,
0 < a < b ), opposite with a = 1, b =
2, k = 3/4 |
 |
the ovoid with profile the Granville
egg ( ,
0 < a < b) , opposite with a = 4, b =
6, k = 4 |
 |
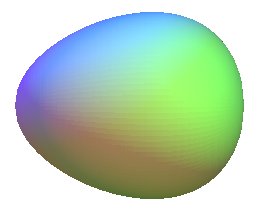the ovoid with profile the Rosillo
curve ( ,
b
= –a, a < c < d ),
opposite with a = 1, c = 2, d = 3 |
 |
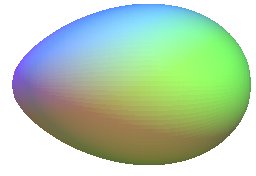A. de Quay proposed 
for k = 3, r = 4, d = 5 (a 
–3,4 ; b  0,5) |
 |
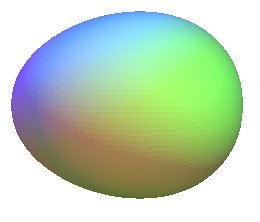Simon Cadrin proposed  ,
with a=–1, b=3 ; Cartesian equation of the profile:  . |
 |
See also the Cartesian ovals, the Ehrhart eggs, the curves of the slider-crank mechanism, the right folia.
For a list of egg-like curves: www.mathematische-basteleien.de/eggcurves.htm
| next surface | previous surface | 2D curves | 3D curves | surfaces | fractals | polyhedra |
© Robert FERRÉOL 2017