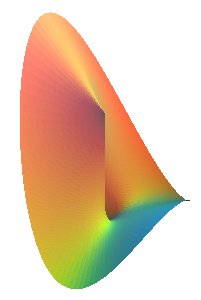
RULED SURFACE WHITH A STRAIGHT DIRECTRIX
| next surface | previous surface | 2D curves | 3Dcurves | surfaces | fractals | polyhedrons |
RULED SURFACE WHITH A STRAIGHT DIRECTRIX

| Studied by Barré in 1916, Buhl in 1944. |
| For surfaces of directrix Oz :
Differential cylindrical caracterisation: Cylindrucal equation: Cartesian paramétrisation: |
A ruled surface is said to be with straight directrix if its generators all pass through a fixed line.
Examples :
- cones (case
where the directrix is reduced to a point),
- conoids
(of which the hyperbolic
paraboloid), case where there is also a director plane,
- conoidal surfaces
(of wich the milk cartoon),
case where there are two straight directrices
- closed
ruled helicoids (of which the right helicoid), .
See also the ruled
surfaces with a director plane.
| next surface | previous surface | 2D curves | 3Dcurves | surfaces | fractals | polyhedrons |
© Robert FERRÉOL 2020