Surface étudiée par Delaunay en 1841, Lindelöf en 1863, Plateau en 1873.

 

Paramétrisation cartésienne :  où  est la paramétrisation de la roulette de Delaunay associée.

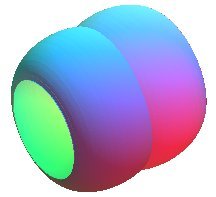
Les surfaces de Delaunay sont les surfaces de révolution engendrées par la rotation des roulettes de Delaunay autour de leur base.

Les surfaces associées à une roulette elliptique sont appelées les onduloïdes, et celles associées à une roulette hyperbolique les nodoïdes.
La roulette parabolique étant la chaînette, la surface associée n'est autre que le caténoïde (cas de la courbure moyenne nulle).

Si on y inclut la sphère, qui en est un cas limite, les surfaces de Delaunay ont la propriété remarquable d'être exactement les surfaces de révolution à courbure moyenne constante ; le cas de la courbure nulle est obtenu pour le caténoïde.

Par conséquent, un film de savon ayant un axe de révolution prend la forme d'une surface de Delaunay.

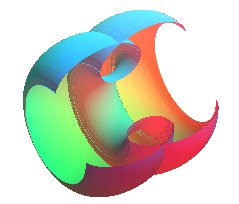
voir aussi : Histoires de bulles et de doubles bulles, La Recherche, N°303 - 11/1997
et www.gang.umass.edu/gallery/cmc/
 

surface suivante

surface précédente

courbes 2D

courbes 3D

surfaces

fractals

polyèdres

© Robert FERRÉOL 2012