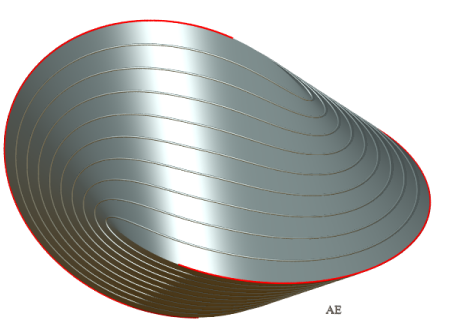
L'oloïde est l'enveloppe convexe de deux cercles orthogonaux passant chacun par le centre de l'autre. Sa surface est une partie de la  surface développable s'appuyant sur les deux cercles (dem : H. POTTMANN, J. WALLNER : Computational Line Geometry, Springer-Verlag Telos (2001) p. 405)
 

Vue de l'oloïde avec les génératrices limitées aux deux cercles directeurs. La surface est invariante par les deux retournements échangeant les deux cercles et donc formée de 2 parties symétriques, ici en rouge et en bleu.  Les axes des retournements sont les deux droites perpendiculaires passant par le milieu des centres des 2 cercles, perpendiculaires à l'axe des centres, et faisant un angle de 45° avec les plans des cercles.

Vue de la surface développable avec les génératrices prolongées, montrant l'arête de rebroussement, composée de 4 branches.

 

Construction géométrique des génératrices. La condition de développabilité est que le plan tangent soit le même tout le long de la génératrice (MN)  (M décrivant le premier cercle et N le deuxième) ; les deux tangentes aux cercles en M et N  sont donc incluses dans ce plan ; mais elles sont aussi chacune incluses dans les plans des cercles, lesquels se coupent en une droite (D) ; les deux tangentes se coupent donc en un point P sur (D), ce qui détermine M connaissant N et vice versa (ceci vaut d'ailleurs pour n'importe quelle surface développable s'appuyant sur deux courbes planes).

 

Si l'on choisit  et , la relation entre u et t est donnée par . La distance MN est constante, égale à . Équation cartésienne de la surface : . Surface algébrique de degré 8. Volume de l'oloïde : . Aire de la surface latérale :  (= aire de la sphère de rayon 1)

Le roulement des deux cercles sur un plan donne le patron de cette surface (modèles réalisés par Robert March) :

 
 

On peut généraliser l'oloïde au cas de 2 cercles orthogonaux de mêmes rayons mais avec une distance quelconque entre les centres. Le cas où les cercles ont le même centre donne un équidomoïde, réunion de 4 portions de cylindres elliptiques.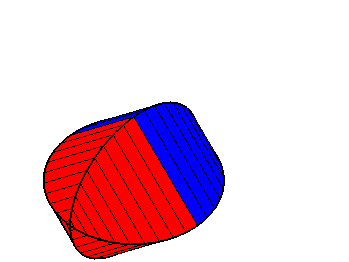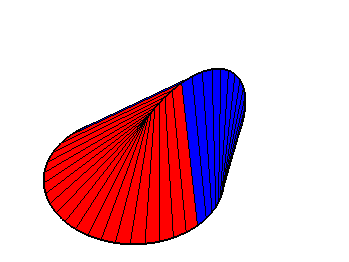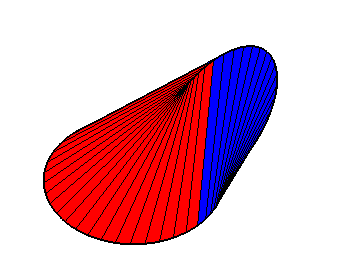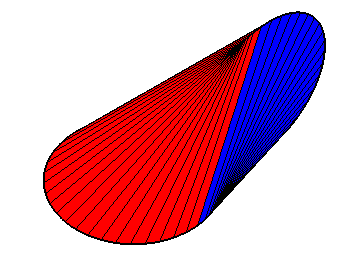

Modèles en papier réalisés par Yves Maniette

 

Ne pas confondre l'oloïde avec le sphéricône, qui est l'enveloppe convexe de deux demi-cerles orthogonaux de mêmes centres. Sa surface est également développable puisque formée de 4 portions de cônes de révolution qui se raccordent "tangentement", mais avec des discontinuités de courbure. On notera aussi que les arêtes sont deux demi-cercles alors que celles de l'oloïde sont des portions de cercles plus grandes.

Liens : Étude mathématique de l'oloïde (donnant entre autres la paramétrisation de la courbe limitant le développement de l'oloïde) Site sur l'oloïde en allemand Physique, jouets et art

surface suivante

surface précédente

courbes 2D

courbes 3D

surfaces

fractals

polyèdres

© Robert FERRÉOL 2016