Cas n = 5/16

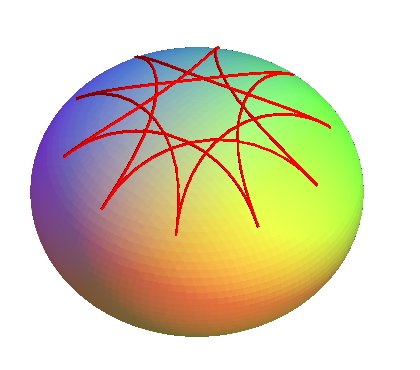
Cas n = 5/7

 
 
 
 

Courbe étudiée par E. Salkowski en 1909, et par J. Monterde en 2009 et en 2024.

 

Paramétrisation cartésienne : ,  ;  où  est l'angle constant entre le vecteur normal  et . Courbe tracée sur la quadrique de révolution : . Abscisse curviligne : . Rayon de courbure constant : . Rayon de torsion : .

Les courbes de Salkowski sont les courbes à courbure constante dont la normale principale fait un angle constant avec une direction fixe (ces dernières courbes étant désignées en anglais par "slant helices", comparer avec les hélices).

Pour , soit , la courbe est tracée sur un ellipsoïde de révolution, et pour , soit , elle est tracée sur un hyperboloïde de révolution.
Dans le premier cas, la projection sur xOy est la même que celle de l'épicycloïde sphérique de paramètres  et  (voir l'article de J. Monterde). La courbe de Salkowski est donc alors formées d'arches dont le nombre est égal au numérateur de 2n si n est rationnel.

Les points de rebroussement étant obtenus pour , soit , on obtient une arche pour , et la courbe complète pour .
 
 

courbe suivante

courbe précédente

courbes 2D

courbes 3D

surfaces

fractals

polyèdres

© Robert FERRÉOL 2024