SINUSOID

| next curve | previous curve | 2D curves | 3D curves | surfaces | fractals | polyhedra |
SINUSOID

| Curve studied for the first time by Roberval in 1636,
under the name "companion of the roulette".
This name was used until around 1850, together with "sine curve", then became sinusoid or sine wave. |
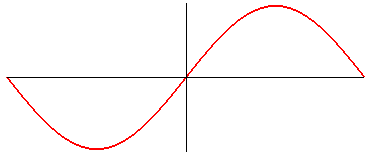 |
Cartesian equation: Transcendental curve. Length on a period, given by an elliptic integral of the second kind: In the case a = b: |
The sinusoid is the trajectory of a movement composed of a sinusoidal motion (i.e. the projection on a line of a uniform circular motion) and of a motion of uniform translation:

If the plane of the sinusoid is winded into a cylinder
of revolution with generatrix Oy and radius nb, then we get
the cylindric
sine wave: .
When n = 1, it is an ellipse of eccentricity ,
and therefore, the expansion of a planar section of a cylinder of revolution
is a sinusoid: concretely, the trace of the edge of a bevelled candle,
rolling on a plane, is a sinusoid:
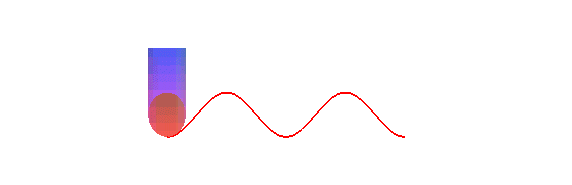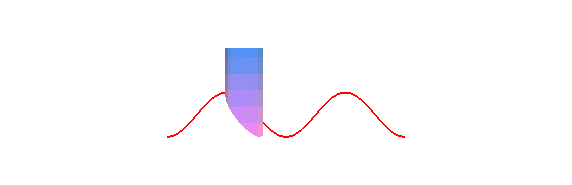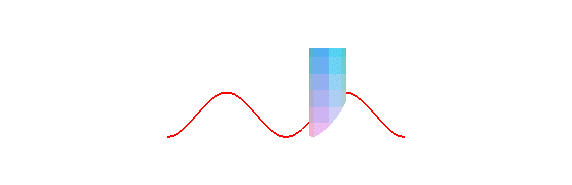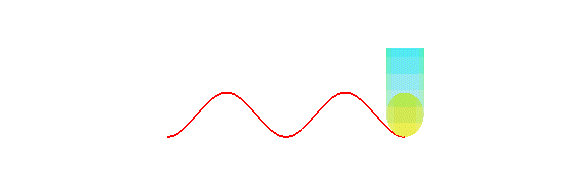
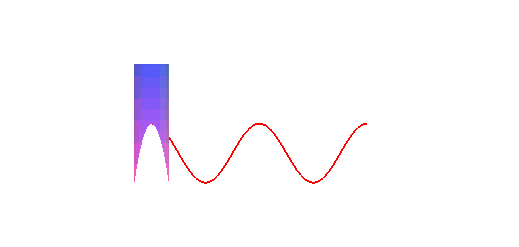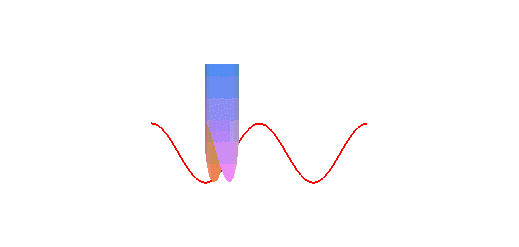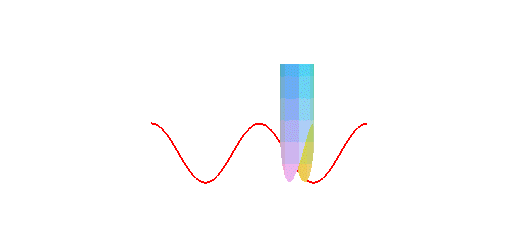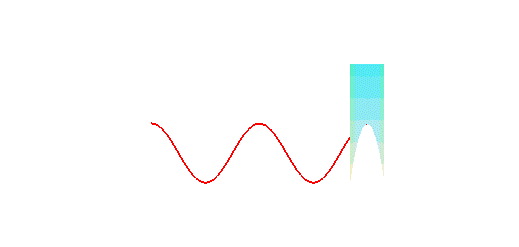
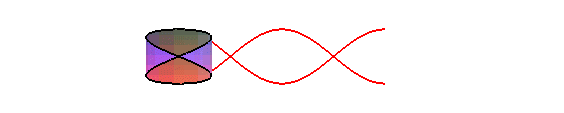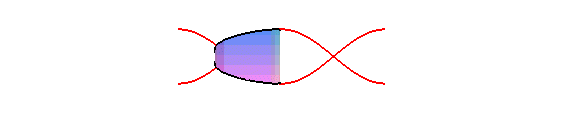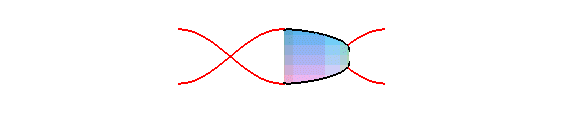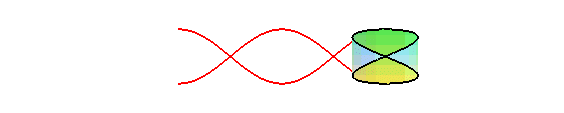
The orthogonal projection of a circular helix on a plane parallel to its axis is a sinusoid.
See also the egg box, the revolution of the sinusoid, the sine surface.

| next curve | previous curve | 2D curves | 3D curves | surfaces | fractals | polyhedra |
© Robert FERRÉOL 2017