Les anneaux de Borromée tirent leur nom d'une célèbre famille de princes italiens de la Renaissance, les Borromée, qui les adoptèrent comme symbole héraldique. Ils sont gravés dans la pierre de leur château, sur l'une des îles Borromée du lac Majeur (isola bella), dans le nord de l'Italie. On retrouve aussi cet entrelac sur des pierres sculptées du IXe siècle environ, à Gotland, une île de la mer Baltique au large des côtes sud-est de la Suède. On pense qu'ils correspondent à des légendes découlant de mythes nordiques. Par ailleurs, les peuples du nord de la Scandinavie connaissent une représentation des anneaux de Borromée en forme de triangles sous le nom de "triangle d'Odin", ou "noeud du tué". Le symbole était également gravé sur les montants des lits utilisés lors des funérailles en mer. Autre nom : entrelacs borroméen. Sites : Knot atlas Site d'Alain Esculier

Représentation par trois couronnes sinusoïdales à trois arches tracées sur trois cylindres à axes parallèles et centrées au sommet d'un triangle équilatéral de côté le double du rayon commun des trois cylindres : Paramétrisation cartésienne :  avec . Représentation par 3 ellipses dont les grands axes sont deux à deux orthogonaux : avec a > b.

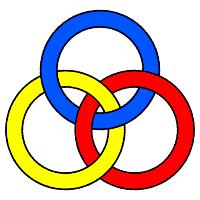
Entrelac senestre : chaque anneau est en dessus du suivant si on tourne dans le sens trigonométrique, donc ils "descendent".

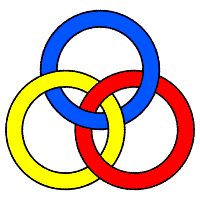
Entrelac dextre : chaque anneau est en dessous du suivant si on tourne dans le sens trigonométrique, donc ils "montent".

Les anneaux de Borromée forment un entrelac de trois noeuds triviaux, connectés comme dans les représentations ci-dessus : ces deux représentations, image miroir l'une de l'autre sont en apparence distinctes, mais donnent en fait des entrelacs topologiquement équivalents (faire passer deux anneaux à l'intérieur du troisième pour passer de l'un à l'autre).

Notons que l'entrelac de Borromée est "alterné" (passage dessus-dessous des cercles entre eux) ; si l'on considère les 2⁶ = 64 façons de modifier les passages des 6 croisements de 3 cercles ayant la même disposition, il existe, en plus du cas borroméen, 4 autres entrelacs topologiquement distincts :
 

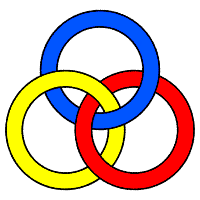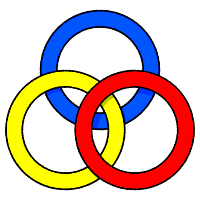
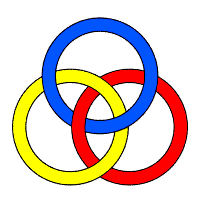
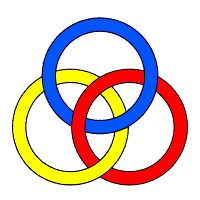
Les 3 anneaux sont libres (rouge sur jaune et bleu, jaune sur bleu) ; entrelac trivial.	Un seul couple d'anneaux enlacés : jaune (entre rouge et bleu) est en fait libre (le tirer vers nord est) !	Deux couples d'anneaux enlacés (rouge bleu et rouge jaune) : on obtient en fait une chaîne de Hopf à 3 anneaux.	Les trois anneaux sont enlacés deux à deux : on obtient l'entrelac premier .

Dans les "vrais" anneaux de Borromée, aucun des couples d'anneaux ne s'interpénètrent ; il suffit de sectionner l'un des trois pour que l'ensemble se disjoigne : la notion générale est celle d'entrelac brunnien.
L'entrelac borroméen est l'entrelac brunnien à plus petit nombre de croisements.
 
 

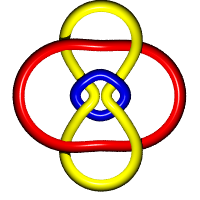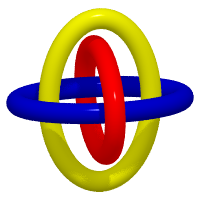
Voici 3 représentations topologiquement équivalentes des anneaux de Borromée (il faut arriver à passer mentalement d'une image à une autre !). La représentation centrale est formée de 3 ellipses situées dans des plans deux à deux orthogonaux. On remarque que la boucle jaune enserre la rouge, qui enserre la bleue, qui enserre la jaune,  etc. à l'infini. On en déduit la projection "plane" de droite : elle possède 8 croisements au lieu de 6, mais avec des passages non alternés.

 

Suite de la déformation. Ce sont toujours des anneaux de Borromée !

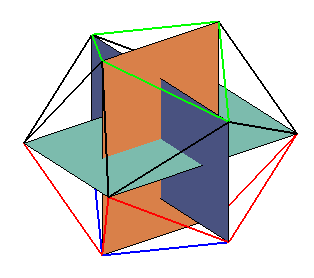
La projection sur la sphère circonscrite des arêtes d'un octaèdre donne trois cercles qui, si on les enlace en les déformant avec passages "dessus-dessous", donne la représentation 3D ci-dessus.   Le fait, qui semble évident, que l'on ne peut pas réaliser la configuration des anneaux de Borromée avec des cercles sans que ceux-ci ne se rencontrent, et sans les déformer, est pourtant très difficile à démontrer (voir Aigner, Ziegler, Proofs from the book, 5. edition, p. 95 à 102).
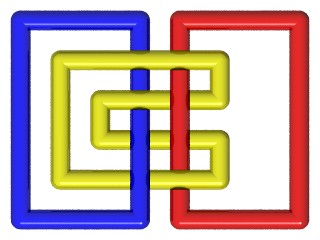
Version cubique du même entrelacs.
En matelotage, la pomme de touline, ou poing de singe, consiste en des anneaux de borromée multiples (en considérant que les 4 anneaux quintuples sont formés d'anneaux fermés). On constate bien que chaque couleur enserre une autre couleur ! Voir la construction sur l'excellent site nico-matelotage.

 

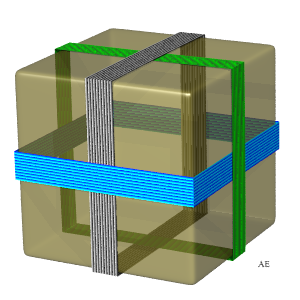
	A gauche, vue d'anneaux borroméens situés dans 3 plans orthogonaux, due à Alain Esculier.  Les 3 anneaux sont elliptiques, d'âmes les 3 ellipses : ,   et ; le diamètre des anneaux est b-a, condition pour qu'ils soient tangents ; la condition pour qu'aux points de tangence, les sections par les plans de coordonnées aient le même rayon de courbure donne  où  est le nombre d'or ; il est remarquable que les 3 rectangles circonscrits aux ellipses sont alors ceux permettant la construction de l'icosaèdre régulier (cf. à droite).
	Autres vues avec anneaux 2 à 2 orthogonaux réalisées par Alain Esculier.

 

Généralisation à n anneaux circulaires dont les centres sont situés aux sommets d'un polygone régulier ; l'enlacement choisi est le passage alternatif dessus-dessous. On constate que lorsque n est impair, les anneaux sont deux à deux non noués comme les anneaux borroméens, et que 3 anneaux consécutifs forment un entrelacs borroméen : étant donc noués, l'entrelac n'est pas brunnien pour n  > 3. Lorsque n est pair, l'entrelac est en quelque sorte "anti-borroméen" : chaque anneau est enlacé avec chaque autre. Images réalisées avec povray par Alain Esculier.

Voir aussi la surface de Seifert associée aux anneaux de Borromée.

Les anneaux de Borromée sont un symbole fort de la cohésion nécessaire d'un groupe : des sociétés commerciales l'utilisent comme logo, des campus universitaires les font trôner à leur entrée et c'est l'un des éléments de la symbolique lacanienne.
 
 
 

Un campus américain : anneaux dextres	Une université italienne : anneaux dextres, avec ruban de Möbius en prime	Une marque de bière : anneaux senestres	Club de sport : anneaux dextres
Union mathématique internationale : anneaux senestres 2 à 2 orthogonaux.	Festival américain de littérature ; FAUX : les 3 anneaux sont 2 à 2 enlacés.	Logo ariel : faux aussi... Et les anneaux semblent impossibles !	Anneaux senestres.

On verra ci-dessous que les anneaux trouvés dans la propriété des Borromée ne sont en fait pas des anneaux de Borromée !
 

Les armoiries de la famille Borromée. Ce sont des faux anneaux de Borromée : l'anneau en haut à gauche est libre, les deux autres enlacés.

Le symbole gravé sur un pot de fleurs ; faux également : les deux anneaux supérieurs sont enlacés, le troisième est libre.

Le symbole sur une gille de jardin ; de nouveau des faux : les anneaux sont deux à deux enlacés.

 

Triangles impossibles de Penrose enlacés en anneaux de Borromée. Création de Francis Casiro, d'après Oscar Reutersvärd. Variante, création d'Alain Esculier. Réseau triangulaire de cercles noués en anneaux de Borromée ;  le pavage obtenu est équivalent à celui de Diane. Réseau carré de cercles noués en anneaux de Borromée

Collage de Julien Garnier, triangle d'Odin.

 

courbe suivante

courbe précédente

courbes 2D

courbes 3D

surfaces

fractals

polyèdres

© Robert FERRÉOL 2022