NOEUD ET ENTRELAC DE BILLARD RECTANGULAIRE
Rectangular
billiard knot and link, rechteckigen Billardknoten und -Verschlingung
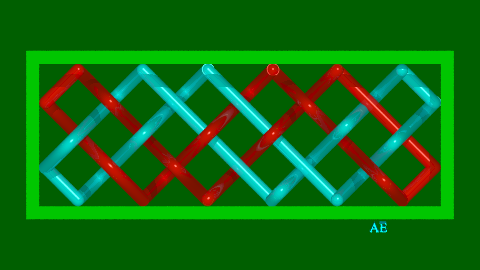
Le " (6,2) "
| courbe suivante | courbe précédente | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
NOEUD ET ENTRELAC DE BILLARD RECTANGULAIRE
Rectangular
billiard knot and link, rechteckigen Billardknoten und -Verschlingung

Le " (6,2) "
| Étudié par Jones
et Przytycki en 1998.
Liens : Tipe sur les trajectoires de billard Construire le (5,3) à la main ! Images réalisées par Alain Esculier. |
Un nœud de billard rectangulaire est le nœud
obtenu à partir d'une trajectoire fermée d'une boule dans
un billard à bords rectangulaires, en modifiant les points de croisements
en passages alternatifs dessus-dessous.
| Si le billard a les dimensions L,L' et la boule
de billard démarre d'un côté de longueur L (hors
coin) avec une trajectoire de pente a par rapport à ce bord,
la trajectoire est fermée ssi le rapport L/L' sur a
est un rationnel p/q (p et q premiers entre eux).
La boule fait alors p rebonds sur les côtés de longueur L, et q sur les côtés de longueur L'. Et il y a en tout |
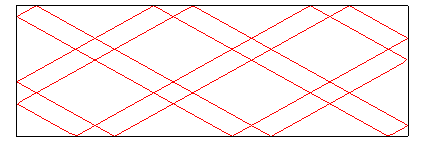
Ici p = 5 et q =3 ; 5 rebonds par bord horizontal, 3 par
bord vertical,
|
| Hormis les cas où elle part d'un coin, la courbe conserve la même topologie, donc donne naissance à un nœud unique, que l'on dira de type (p, q). |
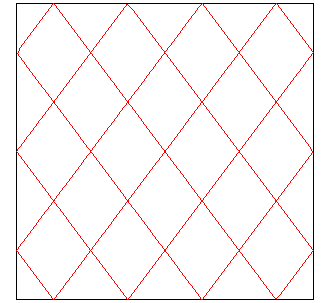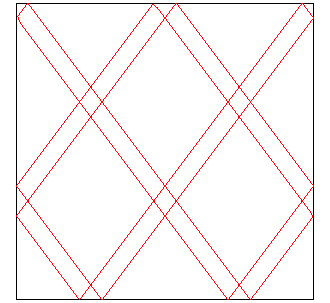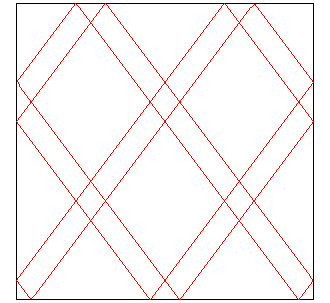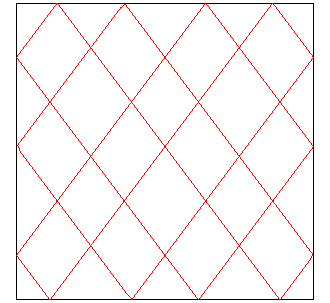 |
| À une dilatation près, on peut se ramener
- au cas où le billard est carré (et la pente vaut p/q), - ou au cas où L/L'=p/q, auquel cas la pente vaut 1 (les croisements se font à angle droit). |
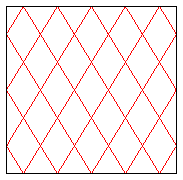 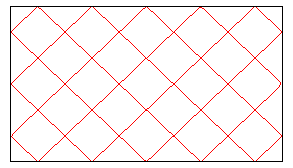 |
| Le nœud de billard de type (p,q) peut aussi s'obtenir
par courbe de Lissajous
plane.
En effet, si c est une fonction continue, paire, strictement décroissante sur Pour Pour |
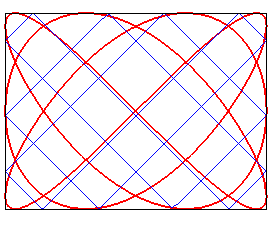
cas p = 4, q = 3 |
| Les alternances dessus-dessous peuvent être obtenues
par une courbe de Lissajous 3D, ou, ce qui est équivalent, par une
trajectoire de bille (non soumise à la pesanteur) dans un billard
parallélépipédique.
Équation avec les notations ci-dessus : Voir à noeud de Lissajous. |
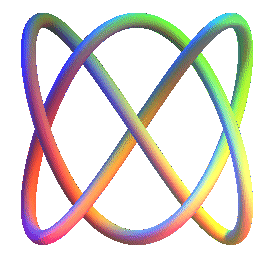 |
Exemples :
| q = 1 : le nœud est trivial | p = 3, q = 2 : on obtient le quatrième noeud premier à 7 croisements. | p = 4, q = 3 , nœud premier à 17 croisements. | p = 5, q = 3 |
 |
 |
 |
 |
| Réalisations artistiques : art bouddhique, islamique, celtique, romain ou maritime ! |
 Photo prise à Katmandou : B. Ferréol. |
Image prise sur le très intéressant blog Nico-matelotage. |

Nœud celtique |
Variantes et généralisations :
1) Pour p et q non premiers entre eux, si l'on trace toutes les trajectoires avec p rebonds régulièrement espacés sur deux côtés opposés, et q rebonds sur les deux autres côtés, on obtient un entrelac à PGCD(p,q) composantes.
Exemples :
| p = 2, q = 2 : on obtient le nœud de Salomon, plus simple des entrelacs non triviaux | p = 3, q = 3 : entrelacs à 12 croisements et 3 composantes, répertorié 12x-3-79 dans knotilus et vu aussi dans katlas.org. Parfois appelé noeud de Salomon triple. | p = 4, q = 2 :
entrelac à 10 croisements et 2 composantes, classé 101 dans knot-atlas. |
p = 4, q = 4 :
nœud de Salomon quadruple. |
|
 |
 |
 |
 |
 |
|
Mosaïque romaine |

Entrelac islamique (Marrakech) |

Motif mongol, que l'on retrouve comme décoration de yourte |

Mosaïque romaine (villa casale) |
 |
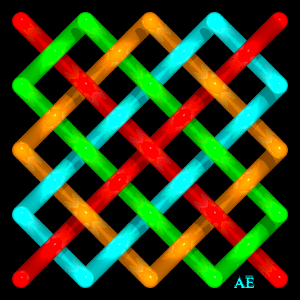
| Le noeud de billard rectangulaire de type (p,q) (premiers entre eux ou non) a pour graphe une grille rectangulaire de p – 1 cases sur q – 1 cases ; ci-contre le cas (5,3). | 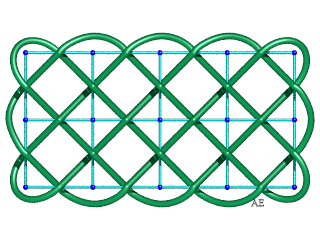 |
2) On peut aussi considérer les courbes obtenues quand la boule de billard part d'un coin. La courbe est alors ouverte, mais peut être fermée de diverses façons ; et on peut aussi effectuer des superpositions.
Exemples dans le cas (3,2) :
La fermeture d'une seule courbe ouverte donne un noeud
trivial, mais la superposition de deux courbes ouvertes est intéressante.
Il s'agit du noeud
de Carrick qui conduit, par fermeture, soit au dix-huitième
noeud premier à 8 croisements : 8.1.18, soit au septième
entrelac premier à 8 croisements et deux boucles : 8.2.7.
 |
 |
 |
 |

Baderne 8.1.18 |

|
Exemples dans le cas (4,3) :
| Si l'on ferme la courbe, on obtient un noeud de trèfle. | Si l'on superpose deux courbes ouvertes et que l'on relie les brins différents, on obtient un noeud à 18 croisements répertorié 18x-1-230179 dans knotilus ; il est utilisé pour la fabrication de paillassons, ou badernes. | Si l'on relie les brins identiques, on obtient un entrelac à 18 croisements répertorié 18x-2 - 410219 dans knotilus. |
 |
 |
 |
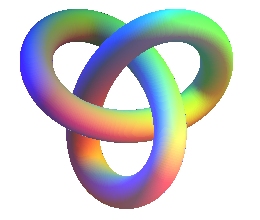 |
 |
|
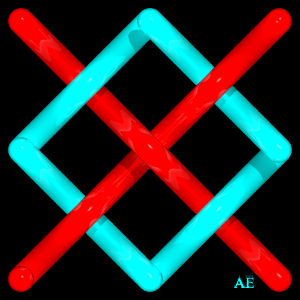
Exemple dans le cas (7,3) :
| Exemple dans le cas (1,1) ; la fermeture donne l'entrelac de Whitehead. | Exemple dans le cas (3,3) : |
 |
 |
3) On peut aussi considérer des croisements dessus-dessous non alternatifs.
On obtient des noeuds dont le nombre minimal de croisements
est inférieur au nombre de croisements de la courbe.
 |
 |
 |
| On a ci-dessus inversé un croisement (en haut à droite) : on remarque q'on pourrait supprimer les deux croisements en haut à droite en raccourcissant la boucle ; on obtient le nœud 5.1.2. | Ici, on remarque que l'on peut supprimer 4 croisements (en haut à droite et en bas à gauche) : comme il reste 3 croisements, on obtient forcément le nœud de trèfle. | Ce nœud a été obtenu en suivant le parcours de la boule de billard avec passage systématique au dessus lorsqu'on traverse un trait antérieur. On peut dénouer en commençant par la fin et le noeud est donc trivial. Ceci fonctionnant dans tous les cas, il existe toujours une configuration donnant le noeud trivial. |
4) On peut généraliser les billards rectangulaires
aux billards polygonaux (non croisés).
Avec des croisements non forcément alternés,
on obtient alors tous les nœuds possibles, et on peut même se restreindre
aux billards de contour un polygone régulier. En effet, tout
nœud a une projection qui est un polygone régulier croisé.
Voir aussi les nœuds polygrammiques.
| Avec un billard triangulaire équilatéral par exemple, on obtient le nœud de trèfle : |
 |
|
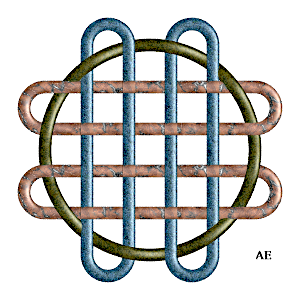
| Entrelac à 4 boucles obtenu dans un billard cruciforme.
A droite, variante avec une boucle supplémentaire, idée d'Alain Esculier. |
 |
 |
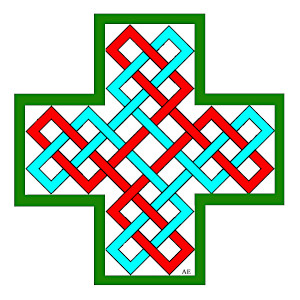
| Cette mosaïque romaine provenant de la villa gallo-romaine de Séviac représente un entrelac qui se trouve être obtenu par le tracé de deux boules dans un billard cruciforme. |
 |
 |
Voir aussi les noeuds de billard cylindriques, ou bonnets turcs, les noeuds celtiques linéaires.

Frontispice de la chapelle de Murato en Corse : il s'agit d'un (22,3).
| courbe suivante | courbe précédente | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
© Robert FERRÉOL 2022