Parallélépipède

PARALLÉLÉPIPÈDE, RHOMBOÈDRE
Parallelepipedon, rhomboedron, Parallelepiped, Rhomboeder

Étymologie : de parallèle et epipedon = surface en grec.

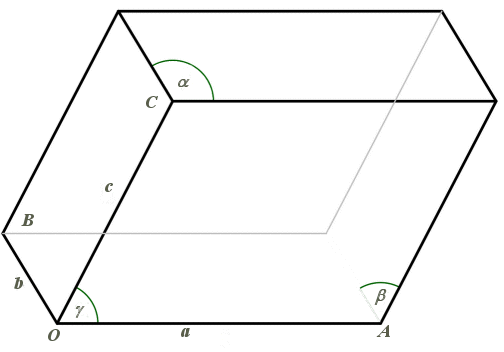
Avec les notations ci-contre, on peut prendre :

,
avec

Volume : .

Cas monoédrique : :

La notion de parallélépipède est la généralisation à l'espace de celle de parallélogramme.
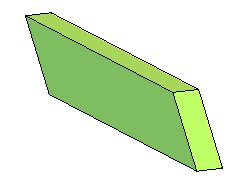
Un parallélépipède est un polyèdre à 6 faces (hexaèdre) se regroupant en 3 paires de faces parallèles. C'est un paralléloèdre, mais ce n'est pas le seul, et un zonoèdre.

Un parallélépipède a toutes ses faces parallélogrammiques, mais la condition n'est pas suffisante (cf. par exemple le dodécaèdre rhombique dont les faces sont des losanges).

Un parallélépipède dont les faces sont des losanges est appelé un rhomboèdre (généralisation à l'espace de la notion de losange) ; CNS : parallélépipède dont toutes les arêtes ont même longueur.
Les faces losanges d'un rhomboèdre sont de trois types caractérisés par les trois angles ci-dessus.

Si de plus toutes les faces sont isométriques, c'est un antidiamant d'ordre 3, ou trapézoèdre trigonal, ou rhomboèdre isoédrique ; CNS parallélépipède monoédrique (faces isométriques).

Un parallélépipède à face contiguës orthogonales est dit rectangle (généralisation à l'espace de la notion de rectangle), apelé aussi cuboïde, ou pavé droit, ou encore, plus familièrement, brique.

Les rhomboèdres rectangles sont les cubes.

Inversement, les parallélépipèdes sont les déformations affines du cube.

La généralisation à la dimension n de la notion de parallélépipède est celle de parallélotope.

Un étrange polyèdre apparaît dans la célèbre gravure d'Albert Dürer "melancolia".
,
Un solide assez ressemblant est ce rhomboèdre à deux sommets opposés tronqués (manipuler à la souris).

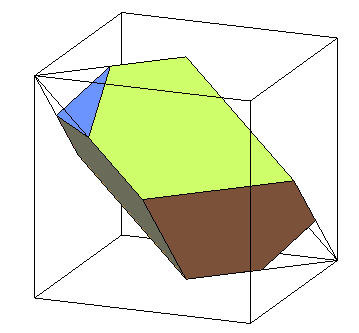Cette vue explique la construction effectuée (6 des 8 sommets sont les centres des faces d'un cube). Les faces du rhomboèdre sont des losanges d'angles 120° et 60°. Cependant ce solide devait être trop vulgaire pour Dürer. D'après mathworld, les angles sont de et , la construction faisant donc intervenir l'ésotérique nombre d'or.
Voir aussi wikipedia.

polyèdre suivant polyèdre précédent courbes 2D courbes 3D surfaces fractals polyèdres

Un étrange polyèdre apparaît dans la célèbre gravure d'Albert Dürer "melancolia".	, Un solide assez ressemblant est ce rhomboèdre à deux sommets opposés tronqués (manipuler à la souris).
Cette vue explique la construction effectuée (6 des 8 sommets sont les centres des faces d'un cube). Les faces du rhomboèdre sont des losanges d'angles 120° et 60°.	Cependant ce solide devait être trop vulgaire pour Dürer. D'après mathworld, les angles sont de et , la construction faisant donc intervenir l'ésotérique nombre d'or. Voir aussi wikipedia.