1) First definition: the Dupin cyclides (in the strict sense) are the surfaces, different from the tori, the curvature lines of which are circles (as an exception, straight lines).
It is conjectured that they are the only surfaces that have a double generation by circles, when the two families of circles are orthogonal.

2) Second definition (directly equivalent to the previous one): they are the surfaces that are envelopes of spheres, in two different ways.
The spheres are then tangent to the cyclide along circles, which are the curvature lines.

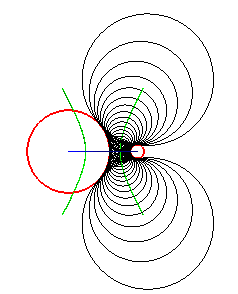
It can be proved that the two focal curves (loci of the centers of the spheres) are conics located in orthogonal planes and such that the foci of one are the vertices of the other; this locus constitutes the focal of the cyclide. These conics are called the focal conics of the cyclide.

There are two cases: the focal conics are...
 

....either an ellipse and a hyperbola, and the cyclide is called "ellipto-hyperbolic". It is then bounded. The two conics have the property that for any pair of points I1 and I2 belonging to both the conics, the two tangent planes to both the conics at I1 and I2 that contain the line (I1 I2) are always perpendicular. To the eyes, these conics seem to intersect with a right angle.
... or two parabolas, and the cyclide is called "parabolic". It is then unbounded. Same visual property as before.

The lines joining two points of each focal conic are the normals of the cyclide (hence the explanation of the previous property: the previous two tangent planes are perpendicular respectively to the two curvature lines at a point of the surface; since the curvature lines are orthogonal, so are the planes).

A) Study of the ellipto-hyperbolic case:
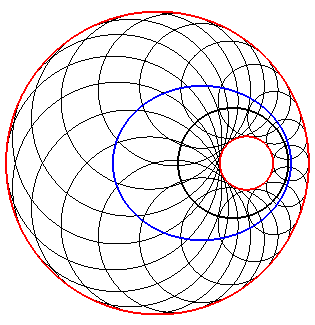
The 4 circles, sections by the planes of the two conics, are called directrix circles of the cyclide (they define it completely).
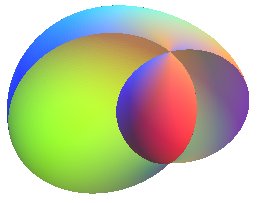
We then get the "ring" cyclide 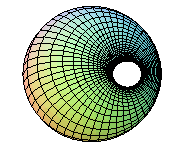 in the following cases:

One of the directrix circles of the plane of the ellipse contains the other one, and the generatrix spheres of the cyclide are externally tangent to these circles; the ellipse is one of the equidistance curves of the two circles. In bold black, trace of the sphere perpendicular to the generatrix spheres (sphere of the inversion swapping the two directrix circles).	The directrix circles of the plane of the hyperbola are outside of one another. The hyperbola is one of the equidistance curves of the two circles.
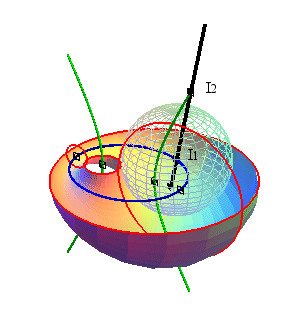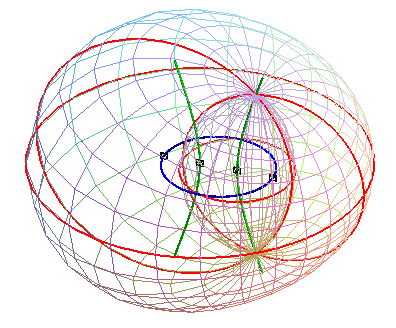
General view with the 4 directrix circles and the 2 focals.	Any normal at M to the cyclide meets the focal ellipse at I1 and the focal hyperbola at I2. We represented the sphere with center I1 passing by M that is tangent to the cyclide, and on the right the sphere with center I2.

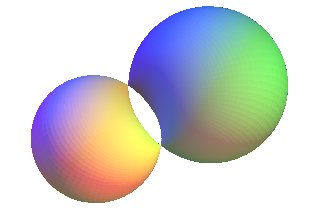
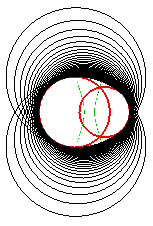
  We get the "spindle" cyclide  in the following cases:

One of the directrix circles of the plane of the ellipse contains the other one and the generatrix spheres of the cyclide are tangent internally to the interior circle; the ellipse is one of the equidistance curves of the two circles.	The directrix circles of the plane of the hyperbola intersect. The hyperbola is one of the equidistance curves of the two circles.	One of the horizontal circles contains the other one, the vertical circles intersect.

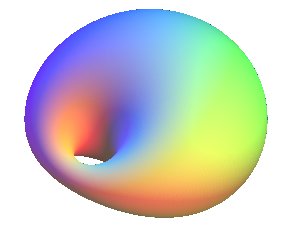
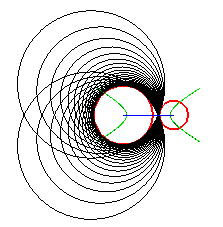
 We get the "horn" cyclide  in the following cases:

secant directrix circles of the plane of the ellipse	directrix circles of the plane of the hyperbola outside of one another	the horizontal circles intersect, the vertical circles are outside of one another

The sphere with center on one of the conic, the envelope of which is the cyclide, is tangent to the cyclide at a circle, intersection between this sphere and the cone with vertex the center of the sphere and directrix the other conic.
 

Equations of the ellipto-hyperbolic cyclides: Focal ellipse and hyperbola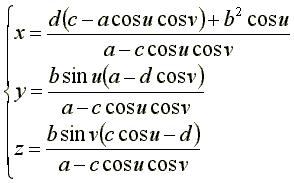:    and  with ,  If  is the current point on the ellipse and the current point on the hyperbola, then the current point on the cyclide is , hence its Cartesian parametrization by the double family of curvature circles: where d is such that the radii of the directrix circles are . Cartesian equation . Rational bispherical quartic surface. Special cases: d = 0  0 < d < b d = b b < d < a d = a d > a symmetric horn cyclide horn cyclide horn cyclide  Not to be mistaken for the pinched torus. ring cyclide ring cyclide with no hole spindle cyclide The tangent spheres are the spheres with center  and radius  and the spheres with center  and radius . The sphere perpendicular to the previous ones has center  and radius . The center of the inversion mapping the ring cyclide onto the torus is .

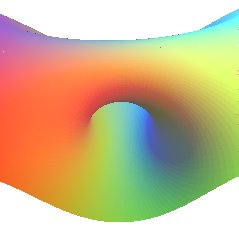
B) Study of the parabolic case.
 

Parabolic cyclides. Focal parabolas: and . The Cartesian parametrization of the cyclide by the double family of curvature circles is: (k ³ 1/2) the radii of the directrix circles being kp/2 and (1 – k )p/2. Planes of the curvatures circles:  and . The normal at M is the line (I1I2) with  on the first parabola, and  on the second one. Cartesian equation: . Rational spherical cubic surface. Special cases: k = 1/2 1/2 £ k < 1 k = 1 k > 1 Ring parabolic cyclide with isometric directrix circles Ring parabolic cyclide Horn parabolic cyclide Horn parabolic cyclide

 

The ring parabolic cyclide with isometric directrix circles is invariant under the action of a half-turn, since a half-turn swaps the two faces. After simplifying by a change of frame, the equation of this cyclide is  (invariant under the action of a half-turn around x = y,z = 0)  Cf. Costa's surface, and the Enneper surface, which have the same property.

3) Third definition: the Dupin cyclides are the envelopes of the tangent spheres (of a certain kind) of two circle-line of a plane, and centered on this plane. The centers of the spheres describe one of the deferent conics.
There exists a second generation of this kind and the centers of the 4 circles obtained (called directrix circles) are the foci of the associated focal conics.

4) Fourth definition, equivalent to the previous one: the Dupin cyclides are the envelopes of spheres with radius R and center M on a conic with focus F such that the distance FM + R, or the distance FM - R are constant.

This allows to visualize the first case by the set of ends of a tight string with constant length hanging from the other end at F and passing by the conic.

This definition allows to easily see that the parallel surfaces of a Dupin cyclide are Dupin cyclides; this property has industrial applications.

5) Fifth definition: the Dupin cyclides are the envelopes of spheres centered on a conic and perpendicular to a fixed sphere centered on the focal axis of the conic. This definition proves that the Dupin cyclides are indeed cyclides. The orthogonal sphere is the fixed sphere of the inversion that leaves the cyclide globally invariant.

6) Sixth definition: if we define the Dupin cyclides in a broad sense as the surfaces the curvature lines of which are circles or straight lines, then they are the inverses of tori, cones of revolution or cylinders of revolution.

The cyclide is a ring cyclide or a spindle cyclide depending on whether the torus has these properties.

It is bounded and algebraic of degree 4 when the center of inversion is not on the torus, unbounded and of degree 3 or 2 otherwise.

The cyclides are the envelope of the family of the inverse spheres of the spheres that are tangent externally to the torus (likewise for the cylinder or the cone).

with the special case of the symmetric horn cyclide (center of inversion located at distance  of O in the plane Oxy)

This definition proves that the ring Dupin cyclides have two other families of circles, inverses of the two families of Villarceau circles of the torus (cf. this article).
 

7) Seventh definition: the Dupin cyclides are the envelopes of spheres tangent to three fixed spheres.

8) Eighth definition: the Dupin cyclides are the stereographic projections of Clifford's torus (included in S³).
 

Some plaster models, taken from this Japanese website:
 

ring cyclide

spindle cyclide

horn cyclide

horn cyclide

ring parabolic cyclide in the case of two isometric directrix circles The outside of this solid is an isometric solid ...

horn parabolic cyclide

Liposomes look like cyclide; see Willmore's torus.

See also this page made by Alain Esculier.
 
 

next surface

previous surface

2D curves

3D curves

surfaces

fractals

polyhedra

© Robert FERRÉOL, Jacques MANDONNET 2017