Cissoid of Diocles

CISSOID OF DIOCLES

Curve studied by Diocles, 180 BC; Fermat; Huygens.
From the Greek Kissos: ivy, probably in reference to the nervures...

Diocles (2nd century BC): Greek mathematician.

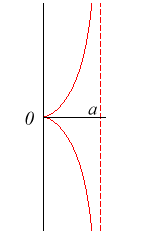Polar equation:

.
Cartesian equation:

(the curve

is studied here).
Rational circular cubic with a cuspidal point.
Rational Cartesian parametrization:

, i.e.

(where t = tanq).
Cartesian tangential angle:

.
Curvilinear abscissa:

.
Radius of curvature:

.
Area between the curve and its asymptote:

The simplest construction of cissoid of Diocles is by double projection on two parallel lines: given two parallel lines (T) and (T') and a point O on (T'), a variable point P on (T) is projected on the point Q on (T'), which in turn is projected on M on (OP): the cissoid of Diocles is the locus of M.

Like all rational circular cubics, the cissoid of Diocles can also be defined as:

- the cissoid with pole O of a circle with diameter [OA] where A(–a,0)...

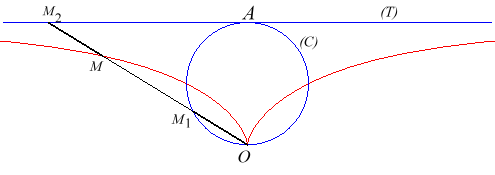
... and therefore also the medial curve of a circle and a straight line

- the pedal of a parabola with respect to its vertex (here the parabola with vertex O and focus F, the symmetrical image of A about O)...

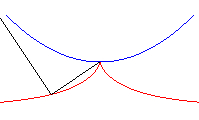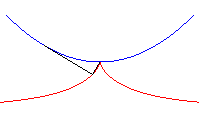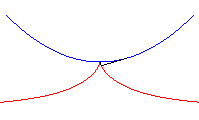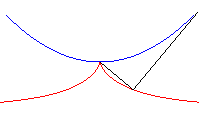.. and therfore also the envelope of circles, centered on a parabola, and passing through its vertex.

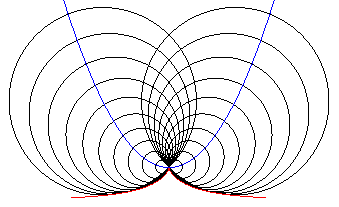- the inverse of a parabola with respect to its vertex (here, the parabola with vertex O and focus A, the circle of inversion being the circle with centre O passing by A)).

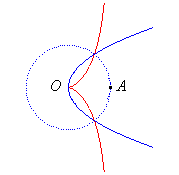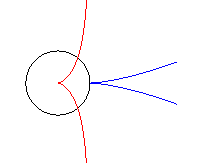
Like all right rational circular cubic, the cissoid of Diocles can be constructed...

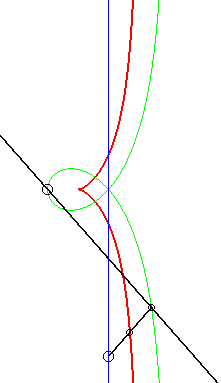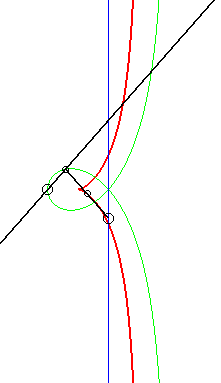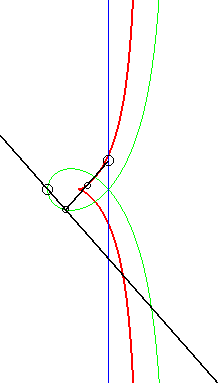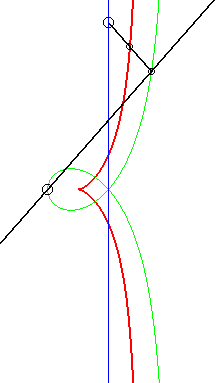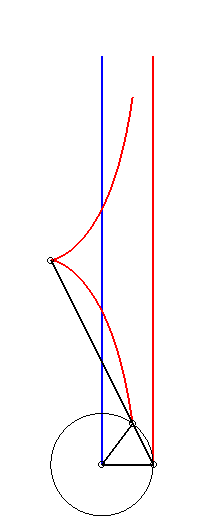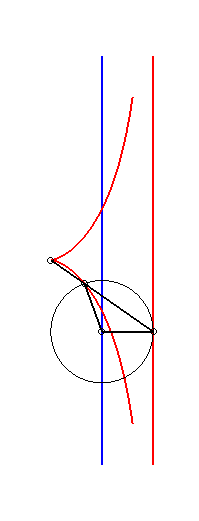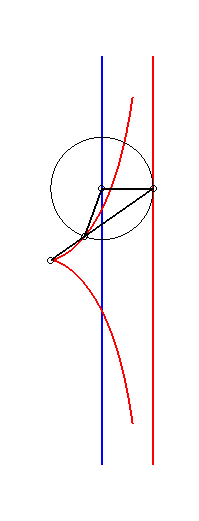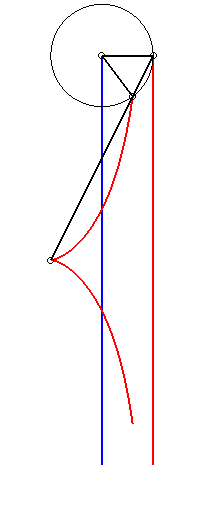...by Newton's set square method: ...as a kieroid

It can also be defined as:

- the locus of the vertex of a parabola rolling without slipping on an isometric parabola such that the two parabolas are outside of one another and their vertices eventually meet (see orthotomic).

- the locus of the focus of a variable parabola with fixed vertex passing by a fixed point (see glissette).

- the orthocaustic of a cardioid with respect to its summit (here, the cardioid with cusp at (a, 0) and summit at (4a, 0)).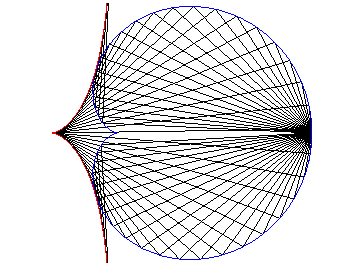

- a Rosillo curve: given a diameter [BC] of a circle and a point P describing this circle, the cissoid is the locus of the intersection point of the perpendicular to [BC] passing through P and the parallel to (CP) passing by B.

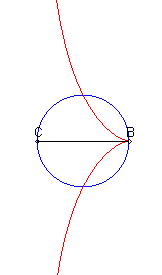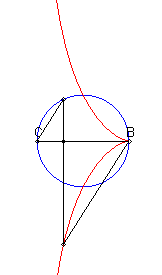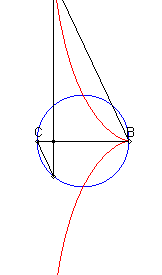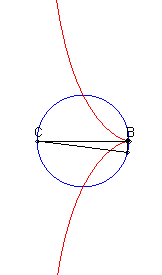Finally, it is a special case of cubic hyperbola and of an ophiuride.

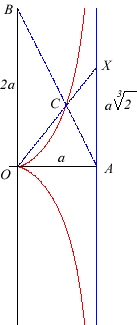The cissoid of Diocles is a duplicatrix: if B is the point with coordinates (0, 2a) and C the intersection point of (C) and (AB), the coordinates of the intersection point X of (OC) and (T) are (a, ).

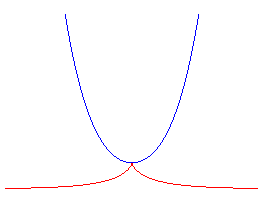The evolute of the cissoid of Diocles is the polynomial quartic .
This figure is not to be mistaken for the plot of the tractrix and its evolute, the catenary. Its polar curve with respect to the circle with centre O and radius a is a semicubical parabola: .

next curve previous curve 2D curves 3D curves surfaces fractals polyhedra

- the cissoid with pole O of a circle with diameter [OA] where A(–a,0)...
... and therefore also the medial curve of a circle and a straight line
- the pedal of a parabola with respect to its vertex (here the parabola with vertex O and focus F, the symmetrical image of A about O)...
.. and therfore also the envelope of circles, centered on a parabola, and passing through its vertex.
- the inverse of a parabola with respect to its vertex (here, the parabola with vertex O and focus A, the circle of inversion being the circle with centre O passing by A)).

- the locus of the vertex of a parabola rolling without slipping on an isometric parabola such that the two parabolas are outside of one another and their vertices eventually meet (see orthotomic).
- the locus of the focus of a variable parabola with fixed vertex passing by a fixed point (see glissette).
- the orthocaustic of a cardioid with respect to its summit (here, the cardioid with cusp at (a, 0) and summit at (4a, 0)).
- a Rosillo curve: given a diameter [BC] of a circle and a point P describing this circle, the cissoid is the locus of the intersection point of the perpendicular to [BC] passing through P and the parallel to (CP) passing by B.