1) Caustique par réflexion de cercle :
 

Paramétrisation cartésienne :  pour le cercle de centre O et de rayon a et la source lumineuse placée en (b, 0). Lorsque la source est sur le cercle (a = b), on obtient la cardioïde : . Lorsque la source est à l'infini (b = ), on obtient la néphroïde : .

Les caustiques par réflexion de cercles sont les enveloppes des rayons issus d'une source lumineuse placée à distance finie ou infinie réfléchis par un cercle.

D'après les propriétés des caustiques, ce sont les développées des orthotomiques de cercles, donc les développées des limaçons de Pascal.

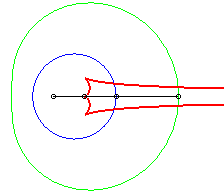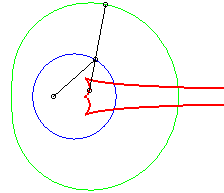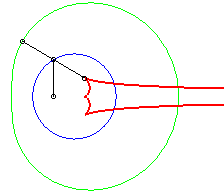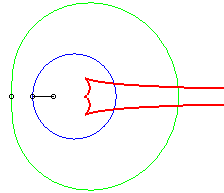
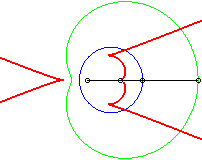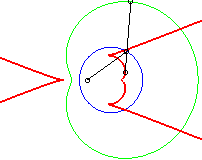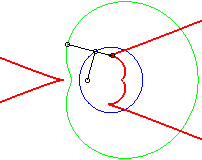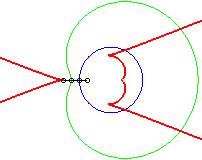
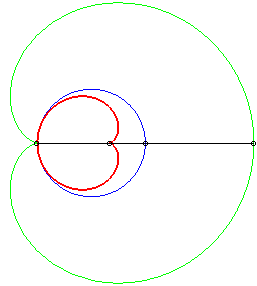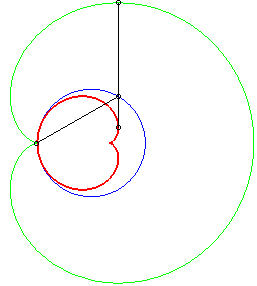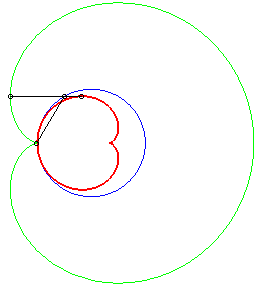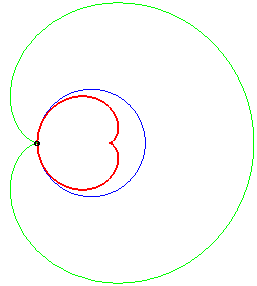
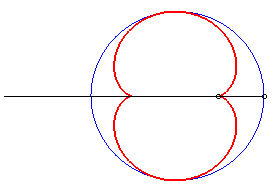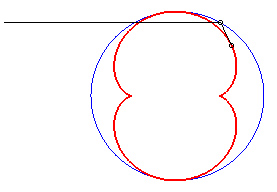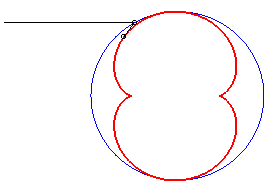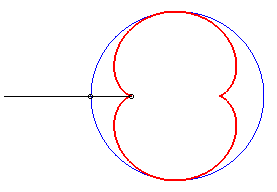
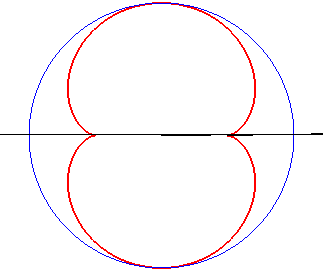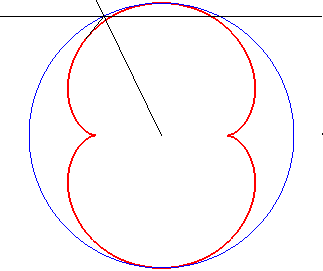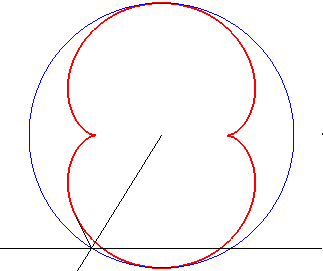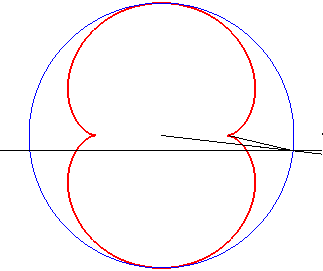
Dans les figures ci-dessous, le cercle est en bleu, le limaçon en vert et la caustique en rouge.
 

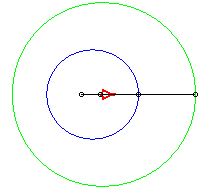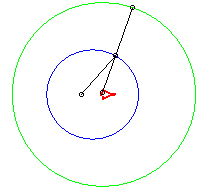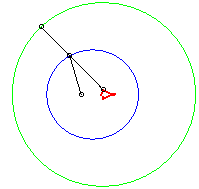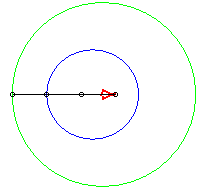
source lumineuse placée en (b,0) avec b = - a / 4

b = - a / 2

b = - 3a / 4

 

b = - a : cas de la cardioïde

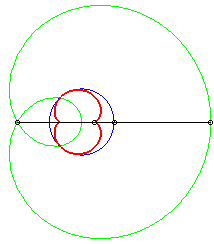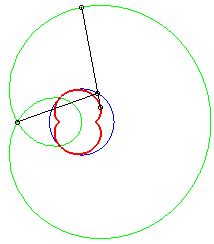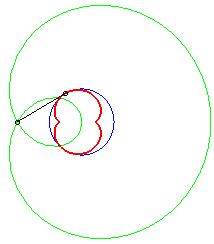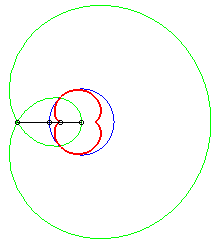
b = - 2a

b = - ¥ : cas de la néphroïde

Les caustiques de cercles s'obtiennent comme section des surfaces caustiques de cônes circulaires pour des rayons à l'infini (le cas de la néphroïde étant obtenu pour un cylindre).

C'est cette propriété qui fait que l'on voit ces courbes dans un récipient conique rempli de liquide éclairé par un faisceau lumineux.

2) Caustique par réfraction complète de cercle, source lumineuse à l'infini.
 

Paramétrisation cartésienne :  pour le cercle de centre O et de rayon a et la source lumineuse à l'infini dans la direction de Ox, et un indice de réfraction égal à n en valeur absolue. Ci-contre, le cas n = 2.
Lorsque n tend vers 1, la courbe précédente tend vers la courbe  qui est bien une néphroïde, caustique par réflexion de cercle.

Le cas d'une source lumineuse à distance finie est traité sur cette page.
 

courbe suivante

courbe précédente

courbes 2D

courbes 3D

surfaces

fractals

polyèdres

© Robert FERRÉOL 2017