Hyperpyramide

HYPERPYRAMIDE

Une hyperpyramide de dimension n est un polytope de dimension n ayant une hyperface (sa base) dont les sommets sont joints par des arêtes à un même sommet S (son sommet) ; les k-cellules de l'hyperpyramide sont les k-cellules de la base, plus, pour toute (k–1)-cellule de la base, la k-pyramide de base cette (k–1)-cellule et de sommet S. Les cellules qui ne sont pas dans la base sont appelées les cellules latérales de l'hyperpyramide.

Par exemple, une hyperpyramide de dimension 4 est formé d'un polyèdre et d'un sommet S. Ses cellules latérales sont les pyramides joignant une face du polyèdre au sommet S. Ses faces sont les triangles joignant une arête du polyèdre à S.

La mesure d'une hyperpyramide est le n-ième du produit de la mesure de sa base par la distance du sommet à l'hyperplan de la base.

Un hypertétraèdre de dimension n est de n+1 façons différentes une hyperpyramide.

La seule hyperpyramide qui soit un polytope régulier est l'hypertétraèdre régulier, mais on désigne en général par hyperpyramide régulière une hyperpyramide dont la base est un polytope régulier et dont le sommet se projette sur l'hyperplan de la base au centre de cette base. Toutes les k-cellules latérales sont alors des hyperpyramides régulières isométriques entre elles.

Un polytope régulier à q hyperfaces se décompose par exemple en q hyperpyramides régulières de bases ces hyperfaces et de sommet le centre du polytope. Ses calottes sont aussi des hyperpyramides régulières.

Exemple :

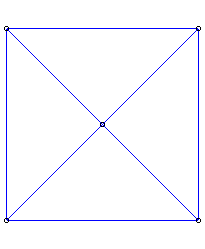
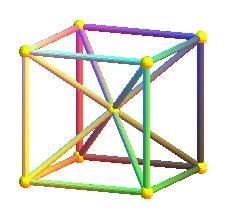
De même qu'une pyramide régulière à base carrée se projette sur le plan de sa base en cette figure : une hyperpyramide de dimension 4 régulière à base cubique se projette sur l'espace de sa base en cette figure : Idem pour l'hyperpyramide régulière à base octaédrique

Remarquer la cellule cubique et six cellules pyramidiques de bases les six faces du cube
cf. l'hyperoctaèdre qui est formé de deux telles hyperpyramides

Comparer avec les hyperprismes.

polyèdre suivant polyèdre précédent courbes 2D courbes 3D surfaces fractals polyèdres

De même qu'une pyramide régulière à base carrée se projette sur le plan de sa base en cette figure :	une hyperpyramide de dimension 4 régulière à base cubique se projette sur l'espace de sa base en cette figure :	Idem pour l'hyperpyramide régulière à base octaédrique
	Remarquer la cellule cubique et six cellules pyramidiques de bases les six faces du cube	cf. l'hyperoctaèdre qui est formé de deux telles hyperpyramides