Équation cartésienne : . Surface algébrique de degré 18. Cas particulier de surface de Lamé. Paramétrisation cartésienne :.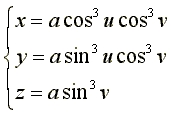

La surface astroïdale est la surface d'équation donnée ci-dessus. Son nom provient de ce que les sections par des plans parallèles aux plans de symétrie sont des astroïdes.

Elle est l'enveloppe des plans coupant les trois axes en trois sommets d'un triangle dont la distance du centre de gravité à O est constante, égale à a / 3.

Elle a les mêmes sommets et les mêmes symétries que la surface de l'octaèdre régulier :.
 

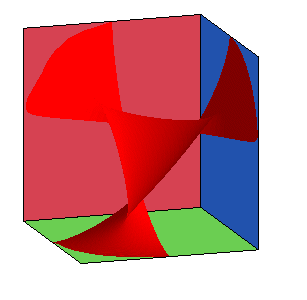
Figure réalisée par Alain Esculier, obtenue par intersection de plans tangents, chacun étant colorié d'une façon différente.

Dans le même genre, l'enveloppe des plans coupant les 3 axes en trois point A,B,C tels que le tétraèdre OABC a cette fois un volume constant est la surface cubique d'équation xyz = a ³.

Autre variante : un disque s'appuie sur les trois faces d'un trièdre trirectangle (penser à une roue de vélo posée contre un coin d'une pièce) ; le centre du disque décrit une portion de sphère, et le plan du disque enveloppe la surface ci-dessous :

© Robert FERRÉOL  2021