Équation cartésienne : ,. Pour a = b : hyperboloïde à deux nappes de révolution. Pour a = b = c : hyperboloïde à deux nappes équilatère. Petit exercice : quel est le type de la quadrique  ? Réponse : par changement de repère O.N. tel que OZ soit la droite x=y=z on tombe sur . Donc un H1 pour , un cône pour , un H2 pour , tous de révolution autour de OZ. Paramétrisation cartésienne               - dont les lignes de coordonnées donnent une famille d'hyperbole et une famille d'ellipses : 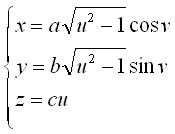, ou , ou encore : .                - dont les lignes de coordonnées sont les lignes de courbure : avec, pour c < b < a : .  Les valeurs u = v = a² donnent les 4 ombilics, de coordonnées . Courbure de Gauss :  où  est la distance de O au plan tangent au point considéré. Cas de l'hyperboloïde équilatère : . Équation cylindrique : . Première forme quadratique fondamentale : . Courbure de Gauss : . Courbure moyenne : .

L'hyperboloïde à deux nappes est la seule quadrique non connexe.

L'hyperboloïde à deux nappes de révolution peut être défini comme la surface de révolution engendrée par la rotation d'une hyperbole autour de son axe transverse. C'est le lieu des points M vérifiant , où F et F' sont les foyers communs à ces hyperboles.
 
 

Vue des lignes de courbure de l'hyperboloïde à deux nappes ; ce ne sont des cercles et des hyperboles que dans le cas de l'hyperboloïde de révolution, sinon, ce sont des biquadratiques. Les 4 points singuliers sont les ombilics.

 

Vue de l'une des deux familles de cercles incluse dans tout H2, même non de révolution, avec les deux ombilics correspondants.

La nappe supérieure de l'hyperboloïde  est utilisée comme modèle du plan hyperbolique. En effet, si on se place dans l'espace de Minkowski où le produit scalaire euclidien est remplacé par le produit , il possède alors une courbure de Gauss constante égale à . Avec la paramétrisation , la première forme quadratique fondamentale est alors .
Voir aussi à spirale de Poinsot.
 

surface suivante

surface précédente

courbes 2D

courbes 3D

surfaces

fractals

polyèdres

© Robert FERRÉOL 2021