SURFACE DE MÖBIUS
Möbius
surface, Möbiussche Fläche
| surface suivante | surface précédente | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
SURFACE DE MÖBIUS
Möbius
surface, Möbiussche Fläche
| Voir les énoncés X 1977 math 2 et agreg 1929. |
Paramétrisation cartésienne :  .
Équation torique :  .
Équation cylindrique :  .
Équation cartésienne : 
(donnant en sus le plan xOz), soit, en simplifiant par y
ou encore 
.
Surface cubique réglée (contient par exemples les droites Ox et Oz). Courbure de Gauss :  .
Droite d'auto-intersection : x = –a ; y = z ; axe de symétrie Ox. Cône directeur de directrice 
qui est une clélie
de paramètre n = 1/2. |
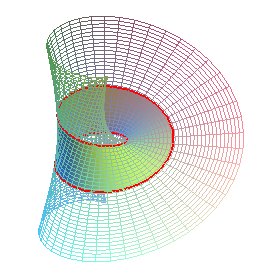
 Portion de surface de Möbius montrant
|
La surface de Möbius est la surface réglée non développable engendrée par la rotation d'une droite dans un plan tournant lui même autour d'une de ses droites avec une vitesse angulaire double de celle de la droite ; c'est donc un cas particulier de rotoïde.
La surface de Möbius est ainsi appelée car
sa portion obtenue pour 
avec 
est
un ruban de Möbius.
On peut aussi la définir comme la surface réglée
ayant pour directrices un cercle (ici, 
),
l'axe de ce cercle (ici, Oz) et une droite inclinée de 45°
sur le plan de ce cercle, se projetant en une tangente au cercle (ici,
x
= –a , y = z ). Possédant deux directrices rectilignes, c'est
une surface conoïdale.
 |
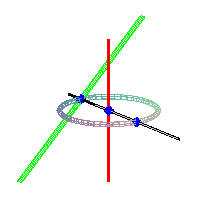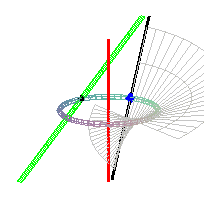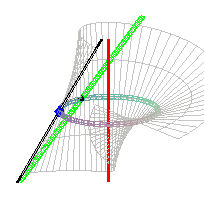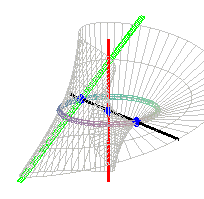Les points d'intersection respectifs de la génératrice
avec le cercle, l'axe rouge et la droite verte sont  . |
La surface de Möbius est d'ailleurs projectivement
équivalente au conoïde de
Zindler ; en effet, le changement 
transforme l'équation homogène 
de la surface de Möbius en l'équation 
de ce conoïde.
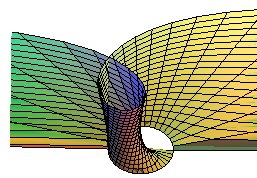
Les sections par les plans horizontaux z = b
sont des strophoïdes,
d'équation  . |
 |
| La section par la sphère de centre O et de rayon R est formée d'une courbe de Viviani et de l'équateur de la sphère. |  |
On peut aussi considérer la surface associée au ruban de Möbius à deux demi-tours (qui n'est pas un ruban de Möbius topologique), où les deux vitesses angulaires (de la droite autour du centre et de la droite sur elle-même) sont égales :
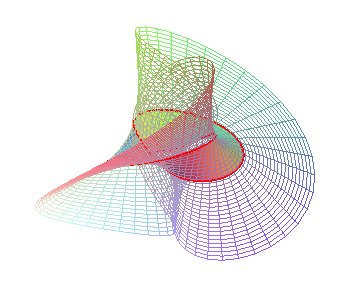
Paramétrisation cartésienne :  .
Équation torique :  .
Équation cylindrique :  .
Équation cartésienne : 
.
Surface quartique réglée. Droites d'auto-intersection : Ox et Oz ; axe de symétrie Ox. Cône directeur de directrice 
qui est une courbe de Viviani. |
| surface suivante | surface précédente | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
© Robert FERRÉOL 2018