fractal suivant fractal précédent courbes 2D courbes 3D surfaces fractals polyèdres

SYSTÈME DE LINDENMAYER
Lindenmayer sytem, Lindermayersches System


Aristid Lindenmayer (1925-1989) : biologiste hongrois. 

Un système de Lindenmayer, ou L-système, consiste en un ensemble E d'objets et une transformation f qui à un objet de E associe une suite finie d'objets de E.
Partant d'un objet x de E, on lui applique f : on obtient la suite d'objets de E à l'étape 1 notée S1 .
Puis on remplace chaque objet de S1 par son transformé par f on obtient la suite à l'étape 2, S2.
On réitère ce processus à l'infini, jusqu'à obtenir une suite infinie S, appelée "point fixe" du système, car elle possède la propriété :

Si on remplace chaque élément de S par son transformé par f, la suite reste inchangée.

par exemple, si E={0,1} et f(0) = 01, f(1) = 10, on obtient
S0 = 0
S1 = 01
S2 = 0110
S3 = 01101001

dont le point fixe S = 01101001100101101001011001101001......... est appelé suite de Thue-Morse.

Si E est l'ensemble des segments du plan, la courbe à l'étape n associée au système est la réunion des segments constituant Sn.

Dans le tableau suivant sont répertoriés de nombreux fractals se construisant par L-systyème.
Un segment en pointillé signifie que ce segment est tracé, mais n'est pas transformé à l'étape suivante.
Deux flèches noires indiquent qu'il faut inverser ses deux extrémités (par rotation).

    F  : avancer d'une longueur a fixée (F initiale de "Forward")
    G : avancer de a sans tracer
    + :  tourner d'un angle t fixé vers la gauche (t initiale de "turn")
    – :  tourner de t  vers la droite
 
Nom du fractal Objet de départ (en pointillé)
et son transformé		 Code L-système Code Maple
Ensemble de Cantor
départ : F
loi : F–>FGF
G–>GGG		 cantor:=proc(A,B,n) if n=0 then [A,B] else 
cantor(A, (2*A+B)/3, n-1),cantor((A+2*B)/3, B, n-1) fi end:
plot([cantor([0,0],[1,0],4)],axes=none,color=red);
Escalier de Cantor oblique
  escalieroblique:=proc(a,b,c,d,n)
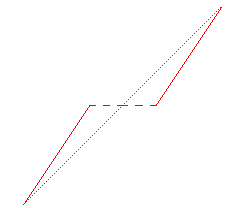
if n=0 then [a,b],[c,d] else 
escalieroblique(a, b, (2*a+c)/3, (b+d)/2, n-1),
escalieroblique((a+2*c)/3, (b+d)/2, c, d, n-1)
fi end:
plot([escalieroblique(0,0,1,1,6)],axes=none,color=red);
Escalier de Cantor droit
  escalierdroit:=proc(a,b,c,d,n)
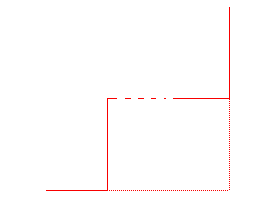
if n=0 then [a,b],[c,b],[c,d] else 
escalierdroit(a, b, (2*a+c)/3, (b+d)/2, n-1),
escalierdroit((a+2*c)/3, (b+d)/2, c, d, n-1)
fi end:
plot([escalierdroit(0,0,1,1,6)],axes=none,color=red);
Courbe de Bolzano- Lebesgue
(t = 1/2 : escalier de Cantor,
t =2/3 : courbe de Bolzano-Lebesgue proprement dite)
  bolzaleb:=proc(a,b,c,d,t,n)
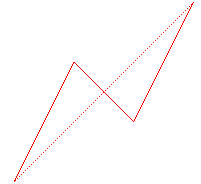
if n=0 then [a,b],[c,d] else 
bolzaleb(a,b,(2*a+c)/3,(1-t)*b+t*d,t,n-1),
bolzaleb((2*a+c)/3,(1-t)*b+t*d,(a+2*c)/3,t*b+(1-t)*d,t,n-1),
bolzaleb((a+2*c)/3,t*b+(1-t)*d,c,d,t,n-1)
fi end:
plot([bolzaleb(0,0,1,1,2/3,5)],axes=none,color=red);
Courbe de Koch
numéro du segment 1 2 3 4
longueur 1/3 1/3 1/3 1/3
angle avec le segment de départ 0° 60° -60° 0°
départ : F
loi :
F–>F+F– –F+F
avec t = 60°

Variante :
loi :

avec t = 30°
koch:=proc(n)
if n=0 then [1] else  L:=koch(n-1):
L1:=  map(z->z/3,L): 
V:=L1[-1]:L2:=map(z->expand(V+z*exp(I*Pi/3)),L1): 
V:=L2[-1]:L3:=map(z->expand(V+z*exp(-I*Pi/3)),L1):
V:=L3[-1]:L4:=map(z->expand(V+z),L1):
[op(L1),op(L2),op(L3),op(L4)]
fi: end:
complexplot([0,op(koch(5))],scaling=constrained,axes=none);		 koch:=proc(A,B,n)
if n=0 then A else 
koch(A, (2*A+B)/3, n-1),
koch((2*A+B)/3, (A+B)/2+I*(B-A)/sqrt(3)/2 ,n-1),
koch((A+B)/2+I*(B-A)/sqrt(3)/2, (A+2*B)/3, n-1),
koch((A+2*B)/3, B, n-1) 
fi end:
complexplot([koch(0,1,4),1],axes=none,scaling=constrained);
Courbe de Koch généralisée
avec 1/4 £ u £ 1/2 ;
u = 1/3 : courbe de Koch,
u = 1/2 : courbe de Césaro
pour Césaro :
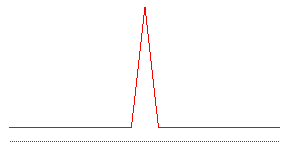
numéro du segment 1 2 3 4
longueur 1/2 1/2 1/2 1/2
angle avec le segment de départ 0° 90° -90° 0°
départ : F

loi :
F–>F+F– –F+F

avec t = arccos(1/2/u-1)
 
kochg:=proc(u,n)
 if n=0 then [1] else 
L:=kochg(u,n-1):p:=nops(L):t:=arccos(1/2/u-1):
L1:=map(z->z*u,L): 
V:=L1[p]:L2:=map(z->expand(V+z*exp(I*t)),L1): 
V:=L2[p]:L3:=map(z->expand(V+z*exp(-I*t)),L1):
V:=L3[p]:L4:=map(z->expand(V+z),L1):
[op(L1),op(L2),op(L3),op(L4)] fi: end:
complexplot([0,op(kochg(0.45,5))],scaling=constrained,axes=none);		 kochg:=proc(A,B,u,n)
if n=0 then A else
kochg(A, (1-u)*A+u*B, u, n-1),
kochg((1-u)*A+u*B, (A+B)/2+I*(B-A)*sqrt(u-1/4), u, n-1),
kochg((A+B)/2+I*(B-A)*sqrt(u-1/4), u*A+(1-u)*B, u, n-1),
kochg(u*A+(1-u)*B, B, u, n-1) 
fi end:
complexplot([kochg(0,1,0.45,4),1],axes=none,scaling=constrained);
Courbe du C
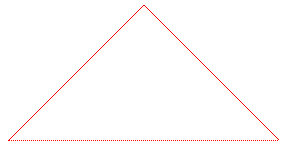
numéro du segment 1 2
longueur 1/Ö2 1/Ö2
angle avec le segment de départ 45° -45°
départ : F

loi :
F–>+F– –F+

avec t = 45°
c:=proc(n) 
 if n=0 then [1] else L:=c(n-1): 
 L1:=  map(z->z*(1+I)/2,L): 
V:=L1[-1]:L2:=map(z->expand(V+z*(1-I)/2),L): 
 [0,op(L1),op(L2)] 
 fi: end: 
 complexplot(c(5),scaling=constrained,axes=none);		 c:=proc(A,B,n)
 if n=0 then A else 
c(A, (A+B)/2+I*(B-A)/2, n-1),
c((A+B)/2+I*(B-A)/2, B, n-1) 
fi end:                                                                                                    complexplot([c(0,1,8),1],axes=none,color=red,scaling=constrained);
Courbe du dragon

Courbe du terdragon
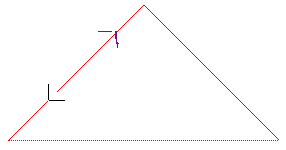
numéro du segment 1 2
longueur 1/Ö2 ; 1/Ö3 1/Ö2 ; 1/Ö3
angle avec le segment de départ 45° ; 30° -45° ; -30°
Départ : F

loi :

avec
t = 45° pour le dragon
t = 30° pour le terdragon
with(plots):with(ListTools):
dragon:=proc(n)
if n=0 then [1] else L:=dragon(n-1):
L1:= map(z->z*(1+I)/2,L):
V:=L1[-1]:L2:=map(z->expand(V+z*(1-I)/2),L):
VV:=L2[-1]:Remove(L2,-1):L2:=[V,op(L2)]:
L2:=map(z->-z+V+VV,Reverse(L2)):
[op(L1),op(L2)] fi: end:
complexplot([0,op(dragon(10))],scaling=constrained,axes=none); 		 dragon:=proc(A,B,n)
if n=0 then [A,B] else 
dragon(A,(A+B)/2+I*(B-A)/2, n-1),
dragon(B,(A+B)/2+I*(B-A)/2, n-1) 
fi end:
plot(map(X ->map(z ->[Re(z),Im(z)],X),[dragon(0,1,8)]),axes=none,scaling=constrained);
Courbe de Peano
(deuxième type)
numéro du segment 1 2 3 4 5 6 7 8 9
longueur 1/3 1/3 1/3 1/3 1/3 1/3 1/3 1/3 1/3
angle avec le segment de départ 0° 90° 0° -90° 180° -90° 0° 90° 0°
départ : F

loi :
F–>F+F–F–F–F
+F+F+F–F

avec t = 90°

 peano:=proc(A,B,n) if n=0 then A else
peano(A,(2*A+B)/3,n-1),
peano((2*A+B)/3,(2*A+B)/3+I*(B-A)/3,n-1),
peano((2*A+B)/3+I*(B-A)/3,(A+2*B)/3+I*(B-A)/3,n-1),
peano((A+2*B)/3+I*(B-A)/3,(A+2*B)/3,n-1),
peano((A+2*B)/3,(2*A+B)/3,n-1),
peano((2*A+B)/3,(2*A+B)/3-I*(B-A)/3,n-1),
peano((2*A+B)/3-I*(B-A)/3,(A+2*B)/3-I*(B-A)/3,n-1),
peano((A+2*B)/3-I*(B-A)/3,(A+2*B)/3,n-1),
peano((A+2*B)/3,B,n-1) 
fi end:
complexplot([peano(0,1+I,3),1+I]),axes=none,color=red,scaling=constrained);
Courbe de Peano
(premier type)		      
Courbe de Péano incomplète, remplissant le carré de Sierpinski
départ : F

loi :
F–>F+F–F–G–F
+F+F+F–F

avec t = 90°

 peanosierp:=proc(A,B,n) if n=0 then [A,B] else 
peanosierp(A,(2*A+B)/3,n-1),
peanosierp((2*A+B)/3,(2*A+B)/3+I*(B-A)/3,n-1),
peanosierp((2*A+B)/3+I*(B-A)/3,(A+2*B)/3+I*(B-A)/3,n-1),
peanosierp((A+2*B)/3+I*(B-A)/3,(A+2*B)/3,n-1),
peanosierp((2*A+B)/3,(2*A+B)/3-I*(B-A)/3,n-1),
peanosierp((2*A+B)/3-I*(B-A)/3,(A+2*B)/3-I*(B-A)/3,n-1),
peanosierp((A+2*B)/3-I*(B-A)/3,(A+2*B)/3,n-1),
peanosierp((A+2*B)/3,B,n-1) 
fi end:
plot(map(X ->map(z ->[Re(z),Im(z)],X),[peanosierp(0,1+I,3)]),axes=none,scaling=constrained);
L-système à trois barres
comprenant
le terdragon
et le contour de l'île de Gosper
  troisbarres:=proc(A,B,n,t,v,u,w)
 if n=0 or abs(B-A)<0.01 then A else P,Q:=(1-t)*A+t*B+I*(B-A)*v,(1-u)*B+u*A+I*(B-A)*w:
 troisbarres(A,P,n-1,t,v,u,w),
 troisbarres(P,Q,n-1,t,v,u,w),
 troisbarres(Q,B,n-1,t,v,u,w) 
 fi end:
dess:=troisbarres(0,1,30,0.1,0.2,0.1,-0.2):
complexplot([dess,1],scaling=constrained,axes=none);
Courbe du triangle de Sierpinski
numéro du segment 1 2 3
longueur 1/2 1/2 1/2
angle avec le segment de départ 60° 0° 60°
 
with(plots): t:=Pi/3:r:=1+2*cos(t):
sierpinski:=proc(n)
if n=0 then [1] 
else L:=sierpinski(n-1):
L1:=map(z->conjugate(z)*exp(t*I)/r,L):
L2:=map(z->L1[-1]+z/r,L): 
L3:=map(z->conjugate(z)*exp(-t*I)/r+L2[-1],L): 
[op(L1),op(L2),op(L3)]: fi end:
complexplot([0,op(sierpinski(5))],scaling=constrained,axes=none);		 t:=Pi/3:r:=1+2*cos(t):
sierpinski:= proc(A,B,n)
if n=0 then [A,B]: 
else P,Q:=A+(B-A)*exp(I*t)/r,B-(B-A)*exp(-I*t)/r: 
sierpinski(P,A,n-1),
sierpinski(P,Q,n-1),
sierpinski(B,Q,n-1) 
fi: end:
plot(map(X ->map(z ->[Re(z),Im(z)],X),[sierpinski(0,1,5)]),
axes=none,color=red,scaling=constrained);
Courbe de Hilbert
(premier type)
X –> +YF–XFX–FY+
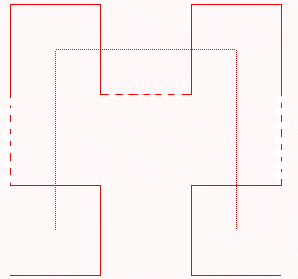
Y –> –XF+YFY+FX–		 hilbert:=proc(A,B,n,e)
if n=0 then (3*A+B)/4+e*I*(B-A)/4,(3*A+B)/4+3*e*I*(B-A)/4,
(A+3*B)/4+3*I*e*(B-A)/4,(A+3*B)/4+e*I*(B-A)/4 else 
hilbert(A,A+e*I*(B-A)/2,n-1,-e),
hilbert(A+e*I*(B-A)/2,(A+B)/2+e*I*(B-A)/2,n-1,e),
hilbert((A+B)/2+e*I*(B-A)/2,B+e*I*(B-A)/2,n-1,e),
hilbert(B+e*I*(B-A)/2,B,n-1,-e) 
fi end:
complexplot([hilbert(0,1,2,1)]),axes=none,color=red,scaling=constrained);
Courbe de Hilbert
(deuxième type)
  hilbert2:=proc(A,B,n)
if n=0 then [A,B] else 
hilbert2(A+I*(B-A)/2,A,n-1),
hilbert2(A+I*(B-A)/2,(A+B)/2+I*(B-A)/2,n-1),
hilbert2((A+B)/2+I*(B-A)/2,B+I*(B-A)/2,n-1),
hilbert2(B,B+I*(B-A)/2,n-1) 
fi end:
complexplot([hilbert2(0,1,4)]),axes=none,color=red,scaling=constrained);
Courbe de Sierpinski  
départ  : A
loi  :
A –> B–A–B,
B –> A+B+A
    angle  : 60º		 sierpinski:=proc(A,B,n)
 if n=0 then [A,B] else 
sierpinski((3*A+B)/4+I*(B-A)*sqrt(3)/4,A,n-1),
sierpinski((3*A+B)/4+I*(B-A)*sqrt(3)/4,(A+3*B)/4+I*(B-A)*sqrt(3)/4,n-1),
sierpinski(B,(A+3*B)/4+I*(B-A)*sqrt(3)/4,n-1) 
fi end:
plot(map(X ->map(z ->[Re(z),Im(z)],X),[sierpinski(0,1,6)]),axes=none,color=red,scaling=constrained);
Saucisse de Minkowski
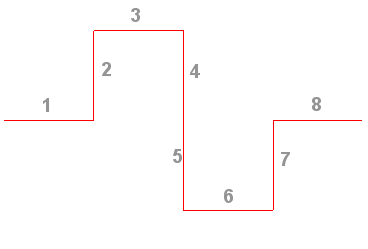
numéro du segment 1 2 3 4 5 6 7 8
longueur 1/3 1/3 1/3 1/3 1/3 1/3 1/3 1/3
angle avec le segment de départ 0° 90° 0° -90° -90° 0° 90° 0°
départ : F
loi :
F–>F–F+F+FF–F–F+F		 mink:=proc(A,B,n)
 if n=0 then A else 
 mink(A,(3*A+B)/4,n-1),mink((3*A+B)/4,(3*A+B)/4+I*(B-A)/4,n-1),
 mink((3*A+B)/4+I*(B-A)/4,(A+B)/2+I*(B-A)/4,n-1),mink((A+B)/2+I*(B-A)/4,(A+B)/2,n-1),
 mink((A+B)/2,(A+B)/2-I*(B-A)/4,n-1),mink((B+A)/2-I*(B-A)/4,(A+3*B)/4-I*(B-A)/4,n-1),
 mink((3*B+A)/4-I*(B-A)/4,(A+3*B)/4,n-1),mink((A+3*B)/4,B,n-1) 
 fi end:
complexplot([mink(0,1,1),1],axes=none,color=red,scaling=constrained);
Courbe de Gosper
numéro du segment 1 2 3 4 5 6 7
longueur 1/Ö7 1/Ö7 1/Ö7 1/Ö7 1/Ö7 1/Ö7 1/Ö7
angle avec le segment de départ 0-a° 60-a° 180-a° 120-a° -a° -a° -60-a°
a = arctan(sqrt(3)/5)).		   gosper:=proc(A,B,n);
u:=evalf(exp(I*Pi/3)):v:=evalf((B-A)*exp(-I*arctan(sqrt(3)/5))/sqrt(7)):
P:=A+v:Q:=P+u*v:R:=Q-v:S:=R+u^2*v:T:=S+v:U:=T+v:
if n=0 then[A,B] else 
gosper(A,P,n-1),
gosper(Q,P,n-1),
gosper(R,Q,n-1),
gosper(R,S,n-1),
gosper(S,T,n-1),
gosper(T,U,n-1),
gosper(B,U,n-1)
fi end: 
complexplot([gosper(0,1,4)],axes=none,color=red,scaling=constrained);
Courbe remplissant le flocon de Koch
  kochp:=proc(A,B,n)

if n=0 then [A,B] else u:=exp(I*Pi/3)/3:

C,D,E,F,G,H:=A+u*(B-A),A+2*u*(B-A),A+(2*u+1/3)*(B-A),A+(2/3+u)*(B-A),A+(B-A)/3,A+2*(B-A)/3:

kochp(C,A, n-1), kochp(C,D, n-1), kochp(D,E, n-1),kochp(E,F, n-1),kochp(G,F, n-1), kochp(H,G, n-1), kochp(H,B, n-1) fi end:

n:=3:plot(map(X ->map(z ->[Re(z),Im(z)],X),[kochp(0,1,n,1)]),axes=none,color=blue,scaling=constrained,thickness=2); 
Arbre
  arbre:=proc(A,B,L,t,n)
local k,M;
k:=nops(L):M:=evalf([seq(L[q]*exp(t[q]*I),q=1..k)]);
if n=0 then [A,B] else
[A,B],seq(arbre(B,B+M[q]*(B-A),L,t,n-1),q=1..k)
fi end:
complexplot([arbre(0,I,[0.7,0.7],[Pi/9,-2*Pi/9],7)],
axes=none,color=COLOR(RGB,0.55,0.2,0),scaling=constrained);
Fougère
  fougere:=proc(A,B,L,t,n)
local k,M;
k:=nops(L):M:=evalf([seq(L[q]*exp(t[q]*I),q=1..k)]);
if n=0 then [A,B] else [A,B],
fougere(B,B+M[1]*(B-A),L,t,n-1),
fougere(B,B+M[2]*(B-A),L,subsop(1=-t[1],t),n-1),
fougere(B,B+M[3]*(B-A),L,t,n-1) 
fi end:
complexplot([fougere(0,I,[0.85,0.33,0.33],[0.05,0.4*Pi,-0.4*Pi],5)]),
axes=none,color=COLOR(RGB,0.1,0.9,0),scaling=constrained);

Voir aussi les attracteurs d'une famille de contractions.
 
fractal suivant fractal précédent courbes 2D courbes 3D surfaces fractals polyèdres

© Robert FERRÉOL 2026