| surface suivante | surface précédente | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
SURFACE DE KUMMER
Kummer
surface, Kümmersche Fläche
| Surface étudiée par Kummer en 1864.
Ernst Kümmer (1810 - 1893) : mathématicien allemand. Lien : catalogue des modèles du laboratoire de mathématiques de Besançon. |
Équation cartésienne : 
où 
de sorte que pqrs = 0 est l'équation de la réunion des faces prolongées d'un tétraèdre régulier centré en O et dont les arêtes sont à distance a de O (cf. figure de droite). Surface quartique. REM : la surface de Kummer passe par les intersections de ces 4 plans avec la sphère  .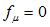
Comparer avec la quartique de Klein. |
 |
La surface de Kummer est la surface d'équation
ci-dessus ; lorsque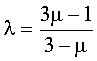 
,
elle possède 16 points singuliers ordinaires (i. e. non dégénérés),
nombre maximal pour une surface quartique ; les 16 points sont réels
pour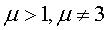 
.
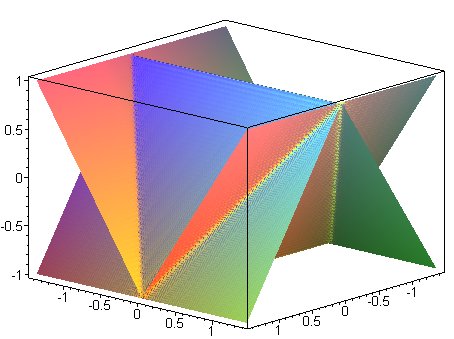
Ci-contre, vue du cas  ,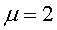
donc  ;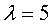
la surface est composée d'un "tétraèdre" central,
prolongé de 4 petits "tétraèdres", eux même
reliés par 6 nappes infinies, en parallèle avec les 6 "arêtes
" du tétraèdre central.
Les 16 points singuliers sont les "sommets" des 4 petits "tétraèdres". |
 |
Le cas  ,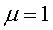
donc 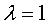 donne
la surface romaine ; les 6
nappes infinies ont disparu, ainsi que le tétraèdre central,
et les 4 petits tétraèdres se sont accolés, faisant
apparaitre 3 segments doubles. |
 |
 |
REM : la surface de Kummer a pour équation dans
un repère tourné de 45° autour de Oz :
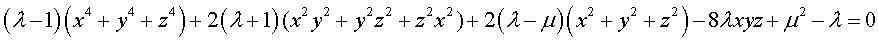
Si l'on remplace les coefficients des termes homogènes
ci-dessus par des coefficients quelconques, on obtient l'équation
générale des surfaces de degré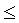 
4 ayant les symétries du tétraèdre ou du cube (voir
à
surface de Goursat).
D'autre part, on peut désigner par "surface de Kummer" toute surface quartique ayant 16 points singuliers ordinaires.
Voir aussi la sextique de Barth, qui est l'équivalent de degré 6 de la surface de Kummer.
Comparer avec la (courbe) quartique
de Klein.
Surface de Kummer par Patrice Jeener |
Surface de Kummer par Alain Esculier,
|
| surface suivante | surface précédente | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
© Robert FERRÉOL 2011
.