Visiera

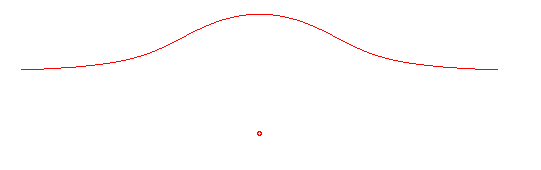
Courbe étudiée par Agnesi (1718-1799).
Visiera : visière en italien.
Le nom de visiera a été donné par Peano en 1887, probablement par analogie avec versiera.

Équation polaire :

.
Équation cartésienne :

.
Cubique circulaire rationnelle droite à point isolé (-> cubique de Sluze)

La visiera est l’antihyperbolisme de la versiera par rapport à sa base et au symétrique de son sommet par rapport à sa base ; dans l’équation ci-dessus, la visiera est l’antihyperbolisme par rapport à O et à x = a de la versiera : .

Comme toute cubique circulaire rationnelle, la visiera peut être définie comme :
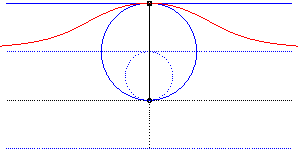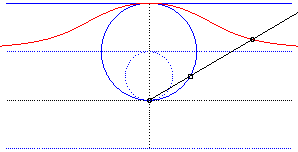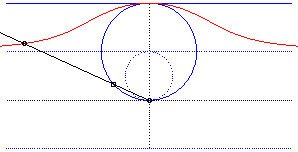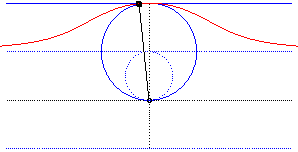
- la cissoïdale d’un cercle et d’une tangente en A à ce cercle, de pôle O point diamétralement opposé à A (ici, A(0,2a)).

- la podaire d'une parabole par rapport au symétrique du sommet par rapport au foyer (ici de la parabole de sommet A et de foyer F(0,a)).

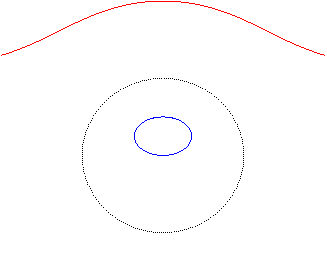
- l’inverse d'une ellipse d'excentricité par rapport à l'un de ses sommets secondaire (ici, de l'ellipse ).

Et comme toute cubique circulaire rationnelle droite, elle peut être construite

- par la méthode de l'équerre de Newton :	- par la construction de Kiernan :

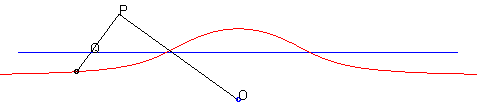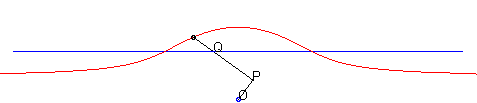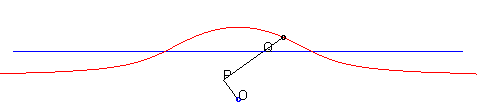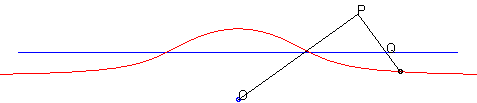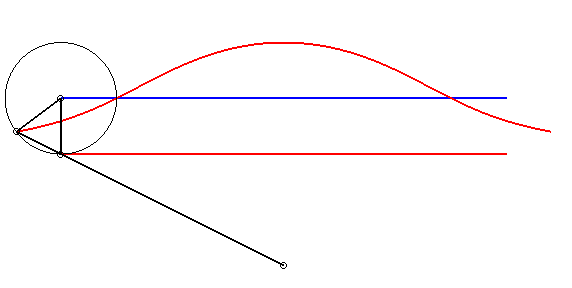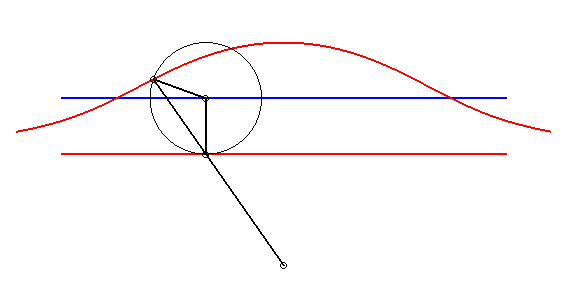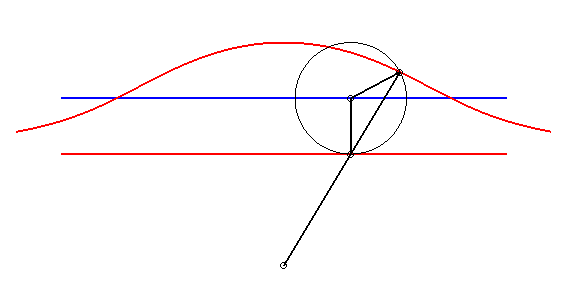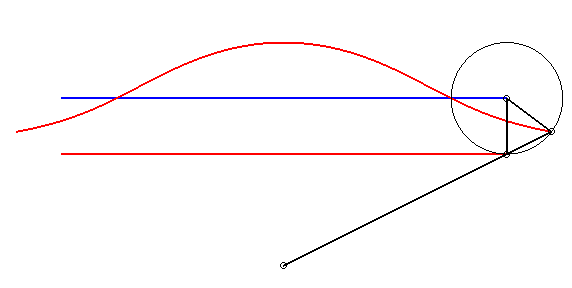Ne pas confondre la visiera avec la conchoïde de Nicomède.

courbe suivante courbe précédente courbes 2D courbes 3D surfaces fractals polyèdres