Équation cartésienne d'un cylindre d'axe orthogonal à (a, b, c) et (a', b', c') : . D'où, pour un cylindre d'axe Oz : Équation cartésienne : . Paramétrisation cartésienne : 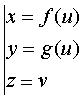. Première forme quadratique fondamentale : . Deuxième forme quadratique fondamentale : . Courbures principales : . Pour une courbe  tracée sur le cylindre : Rayon de courbure géodésique : . Rayon de courbure normal : .

Les cylindres (ou surfaces cylindriques) sont les surfaces réglées dont les génératrices ont une direction fixe  .
Une courbe tracée sur le cylindre et rencontrant toutes les génératrices (par exemple une section par un plan non parallèle aux génératices) s'appelle une directrice du cylindre ; il existe un unique cylindre de direction et de directrice données.

Condition nécessaire et suffisante : surface globalement invariante par toute translation de direction .
On peut aussi considérer qu'un cylindre est un cône dont le sommet se trouve à l'infini.
Les cylindres sont des surfaces de translation, des surfaces développables, et des surfaces moulures.

Les lignes de courbure en sont les génératrices et les sections perpendiculaires aux génératrices.

Le mot cylindre est aussi utilisé dans un sens topologique pour désigner toute surface homéomorphe au cylindre de révolution, ou, ce qui revient au même, à une sphère moins deux points. Par exemple, un ruban ouvert avec un nombre pair de demi-tours est topologiquement un cylindre.

Exemples : cylindre de révolution, cylindre elliptique, parabolique, hyperbolique.

Voir aussi les chaînettes de cylindre.
 
 

surface suivante

surface précédente

courbes 2D

courbes 3D

surfaces

fractals

polyèdres

© Robert FERRÉOL  2020