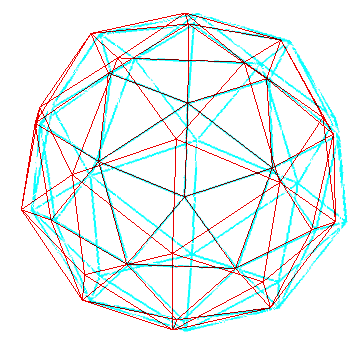
Anaglype à regarder avec des lunettes rouge (à gauche) et bleu (à droite).
| polyèdre suivant | polyèdre précédent | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
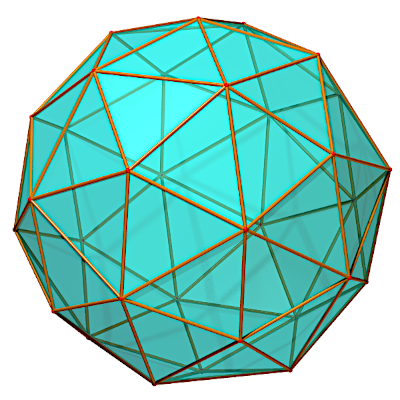
PENTAKI-DODÉCAÈDRE
Pentakis dodecahedron, Pentakisdodekaeder
|
.
Anaglype à regarder avec des lunettes rouge (à gauche) et bleu (à droite).
|
|
| Famille | polyèdre semi-régulier de deuxième espèce ou polyèdre de Catalan | ||
| Historique | étudié par Catalan en 1862 | ||
| Autre nom | pentadodécaèdre ou dodécaèdre à toits | ||
| Dual | icosaèdre tronqué | ||
| Faces | 60 triangles isocèles d'angle au sommet  . |
||
| Sommets | 12 sommets de degré 5, de code de Schläfli 35 et 20 sommets de degré 6 de code de Schläfli 36 | ||
| Arêtes | 60 arêtes de longueur a et 30 arêtes
de longueur 
(celles du dodécaèdre de base) |
||
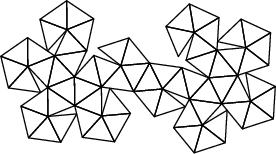
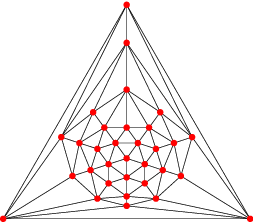
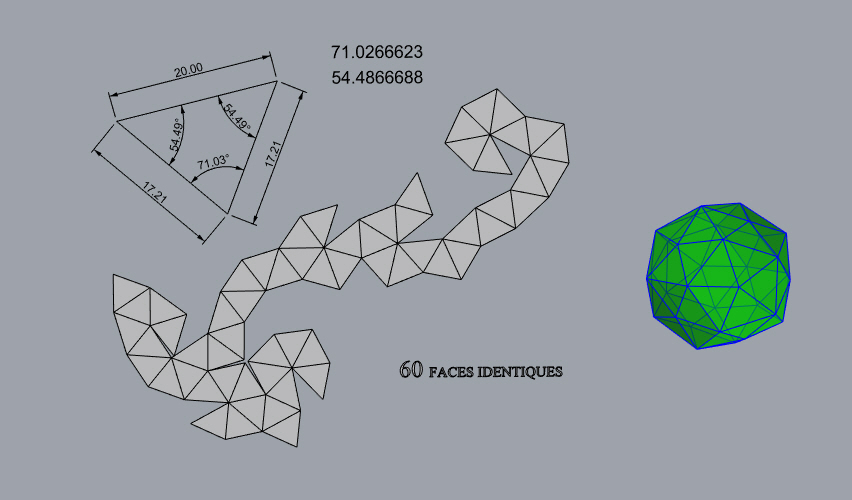
| Patron, graphe, et 3-coloriage |
   |
||
| Diamètres | sphère inscrite : 1,45 a ; sphère circonscrite ...a ; | ||
| Mensurations | volume : 
aire :  |
||
| Construction | dual de l'icosaèdre tronqué
|
||
| Groupe des isométries | = celui de l'icosaèdre. |
| Abat-jour Leroy-Merlin, structure gonflable en forme de pentaki-dodécaèdre... |  |
 |
| Pentaki
-dodécaèdre adouci : |
 |
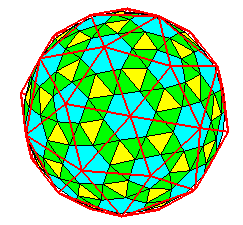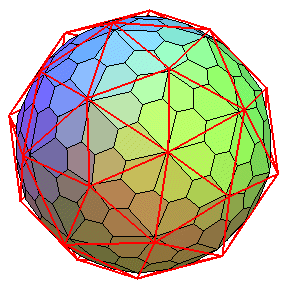
Le dual du précédent.
Voir une superbe réalisation en bois par Roland Gagneux.  |
 |
 |
| Divers polyèdres obtenus par augmentation sur
les faces du dodécaèdre régulier.
En prenant a = 1 pour l'arête du dodécaèdre, si G est le centre d'une face du dodécaèdre, on a  .
Pour le sommet de la pyramide, on prend  .
On obtient successivement : - pour  ,
un polyèdre non convexe à faces équilatérales
rentrantes,
- pour k = 1 , le dodécaèdre (angle en M des triangles : 72°) - pour  ,
le polyèdre de l'encadré suivant (angle en M des triangles
:  )
- pour  ,
le pentaki-dodécaèdre (angle en M des triangles
:  ),
- pour  ,
le triacontaèdre
rhombique (angle en M des triangles :  ),
- pour  ,
un polyèdre à faces équilatérales sortantes
(non convexe). |
 |
| L'intersection de 10 prismes hexagonaux réguliers
pleins dont les axes sont les 10 diagonales d'un dodécaèdre
(ou les 10 diagonales faciales d'un icosaèdre) forme un solide dont
la surface est un polyèdre équivalent au pentaki-dodécaèdre,
obtenu pour
dans la définition précédente.
Remarquer que chacune des 6 faces d'un prisme fournit 6 faces du polyèdre, qui possède donc bien 60 faces.
|
 |
| polyèdre suivant | polyèdre précédent | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
© Robert FERRÉOL 2024
fois l'arête b du pentagone.
