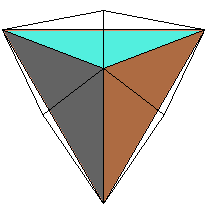
triaki-tétraèdre

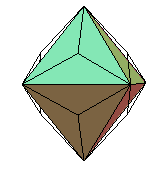
triaki-octaèdre
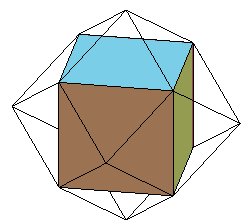
dodécaèdre rhombique
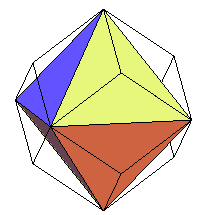
idem
| polyèdre suivant | polyèdre précédent | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
POLYÈDRE AUGMENTÉ
Augmented polyhedron, erweitertes Polyeder
| Un polyèdre est dit être obtenu par augmentation (ou accroissement) à partir d'un polyèdre (P0) s'il résulte du "collage" sur une de ses faces d'un autre polyèdre ayant une face isométrique à la sienne. Il faut bien sûr que les deux polyèdres collés ne se rencontrent pas. Lorsque l'opération est renouvelée deux, trois... fois, on parle de bi-, tri-...augmentation. |
Si S0, F0,
A0 sont les nombres de sommets, de faces
et d'arêtes de (P0), et S1,
F1, A1
les nombres de sommets, de faces et d'arêtes du polyèdre collé,
et n l'ordre de la face collée, le nombre de sommets, de
faces et d'arêtes du polyèdre augmenté (ou accru)
sont :
S = S0 + S1
– n
F = F0 + F1
– 2
A = A0 + A1
– n
Exemples :
- les 5 polyèdres réguliers
augmentés sur chaque face d'ordre n d'une pyramide régulière
à base d'ordre n, dont la hauteur est choisie de sorte que
le polyèdre obtenu ait des angles dièdres égaux fournissent
5 des 13 polyèdres de Catalan.
- une deuxième augmentation
réunissant deux faces contigües de pyramides en fournit 2 autres.
- l'augmentation du cuboctaèdre
et de l'icosidodécaèdre en fournit encore 2.
| Polyèdre de départ |
|
|
|
| première augmentation |

triaki-tétraèdre |

|

triaki-octaèdre |
| deuxième augmentation | On obtiendrait ici le cube. |

dodécaèdre rhombique |

idem |
|
|
|
|
|
|
| première augmentation |
pentaki-dodécaèdre |
triaki-icosaèdre |
||
| deuxième augmentation |
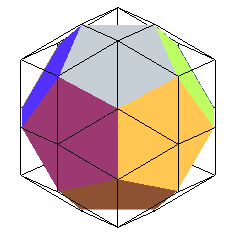
triacontaèdre rhombique |
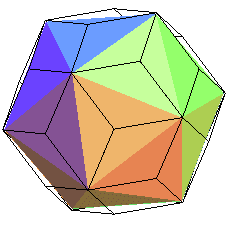
idem |
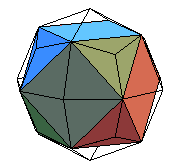
|
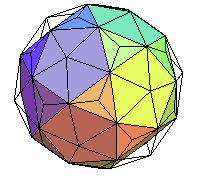
hexacontaèdre trapézoïdal |
- Le tétradécadeltaèdre
et l'hexadécadeltaèdre , ainsi que le triacontahexaèdre
tétragonal sont aussi obtenus par augmentation.
Comparer avec la troncature.
| polyèdre suivant | polyèdre précédent | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
© Robert FERRÉOL
2023