ENCYCLOPÉDIE DES FORMES MATHÉMATIQUES REMARQUABLES
Ce site sur les formes mathématiques est issu d'un
petit résumé commencé en 1993, destiné à
des élèves de math sup désireux d’avoir un récapitulatif
des courbes classiques dont quelques exemples parsemaient mon cours.
Ce résumé a commencé à prendre
du volume, et j’ai pensé que bien que le sujet ne soit pas particulièrement
à la mode, il pourrait intéresser, d'où ce site.
Les courbes et les surfaces m'ont fait découvrir
pas mal de trésors connus de nos prédécesseurs et
que nous avons tendance à oublier. J'ai même eu l'impression
que les anciens avaient une vue beaucoup plus abstraite et générale
de ces objets que celle que nous avons aujourd'hui.
Une note plus contemporaine est donnée par les
fractals qui auraient certainement enthousiasmé les anciens.
Je remercie dans cette entreprise :
- Alain ESCULIER, qui me donne
de judicieux conseils pour la réalisation des animations, et réalise
toutes les figures de qualité utilisant le logiciel povray.
- Pierre LAMBERT, ancien professeur
au lycée de Montmorency, qui profite de sa retraite pour mettre
au clair toute cette vieille géométrie qu'il est encore l'un
des rares à maîtriser parfaitement (mais aussi les maths "de
maintenant"). Je lui dois pas mal de propriétés présentées
ici, mais il est en train de rédiger des notes plus complètes
que j'espère qu'il pourra publier.
- Jacques MANDONNET, mon professeur
en terminale puis ex-collègue en prépa, qui a fait beaucoup
de figures et animations et m'a donné de nombreux conseils en informatique.
- Jacques
BOUTELOUP, qui m'a bien mis au point sur la notion de courbe algébrique.
- François RIDEAU, qui m'a prêté
de nombreux livres rares et anciens qu'il conserve amoureusement, dont
le Gomes Teixeira.
- Robert MARCH, enseignant à
l’École d’Architecture Paris-Val-de-Seine, qui a réalisé
certaines des illustrations et m'a donné de très bonnes idées.
- Mon cousin par alliance Christoph
SOLAND, et Jean-Claude CHASTANG ,
tous deux fans d'ovales de Descartes, l'un en Suisse, l'autre aux États-Unis.
,
tous deux fans d'ovales de Descartes, l'un en Suisse, l'autre aux États-Unis.
Et je remercie WORD, NETSCAPE COMPOSER, MAPLE, et ILLUSTRATOR,
qui m'ont permis de réaliser quelque chose que je n'aurais même
pas imaginé en 93.
MODE D'EMPLOI
Les fiches sont regroupées en 5 thèmes :
les courbes 2D, les courbes 3D (ce qui fait plus "in" que courbe plane
et courbe gauche...), les surfaces, les fractals et les polyèdres.
Chaque fiche commence par l'intitulé de la forme
que l'on va décrire.
Certaines formes qui m'ont paru devoir figurer dans ce
répertoire n'avaient pas de nom reconnu, du moins en français.
J'ai donc usé d'un droit de baptême, et si vous n'êtes
pas d'accord, faites le moi savoir !
Il s'agit par exemple de : AFC,
boite
à œufs,
bouche,
courbe
de la crêpe , courbe
de filature, courbe du
nageur, poisson, serpentine
droite, courbe solénoïdale,
talus,
torpille.
L’intitulé est toujours écrit au singulier,
mais dans le corps de l’article, doit-on parler de la forme au singulier
ou au pluriel ? Quand ses divers représentants sont tous semblables
(dans un sens que nous allons essayer de définir), on a tendance
de parler de cette forme au singulier : la parabole, l’ellipse, l’ellipsoïde
etc. Dans le cas contraire, on en parle plutôt au pluriel : les coniques,
les ovales de Descartes.
Quel sens donner alors au mot semblable ? Pas son sens
mathématique, puisque, si les paraboles sont toutes semblables entre
elles au sens mathématique, ce n’est pas le cas des ellipses. J'ai
donc étendu le sens de semblable à " image par une transformation
affine ". Avec cette définition, j'ai été obligé
de parler des strophoïdes obliques par exemple, bien qu’elles
aient toutes un peu la même tête, mais je dis la strophoïde
droite...
J'ai eu aussi quelques problèmes avec le genre
des noms de courbes et surfaces en " oïde " (du grec eidos : apparence),
qui change suivant les auteurs. Je n'ai pas fait d’exception à la
règle générale qui semble se dégager : féminin
pour une courbe (une deltoïde, une ovoïde), masculin pour une
surface (un caténoïde (bien que le Larousse le donne féminin),
un onduloïde, un ovoïde).
Sont indiqués ensuite les mathématiciens
qui ont étudié l’objet, avec la date correspondante. N’étant
pas spécialiste d’histoire des mathématiques, je me suis
contenté de transcrire les informations des diverses sources, en
particulier de [YATES] ; signalez-moi
les erreurs, svp.
Suit une étymologie succincte de l’intitulé.
J'ai indiqué l’origine de la plupart de ses composants sauf celles
qui semblent évidentes. Je n'ai par exemple pas dit que le mot cercle
vient de circulum qui signifie cercle, ni répété qu’oïde
signifie : en forme de.
Dans la suite, plus mathématique, j'ai essayé
de concilier la rigueur moderne, avec l’élégance et la concision
des expressions de la géométrie traditionnelle. Par exemple,
je parle du " lieu du point M astreint à telle condition"
et non pas de " l’ensemble des points M ... ". Et je parle
de
l’équation cartésienne (ou polaire) bien qu’il
n’y en ait pas qu’une.
D'autre part, le cadre géométrique est
la géométrie affine réelle. Mais lorsqu'on parle de
point à l'infini, ou de point complexe, on considére le prolongement
dans le complété projectif réel ou complexe. Cependant,
distinguer les courbes de 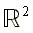 ,
de
,
de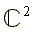 , de
, de 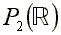 et de
et de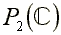 conduit
à des lourdeurs inacceptables.
conduit
à des lourdeurs inacceptables.
En encadré j'indique donc tout d’abord la carte
d’identité de la forme, ou, pour être plus exact, d’un modèle
de la forme. La définition générale qui suit donnera
précisément l’ensemble de tous les objets qui ont pour nom
celui de l’intitulé, mais dans la carte d’identité, n’est
décrit qu’un sous-ensemble représentatif, associé
au repère considéré ; autrement dit, ce que j'annonce
comme équation cartésienne n'est en général
que l'équation cartésienne
réduite. Par exemple
pour les cercles, je prends les cercles de centre O et de rayon
R.
Tous les objets de l’ensemble doivent être semblables (au sens mathématique)
à l’un des objets du sous-ensemble. Mais je ne suis pas allé
jusqu’à mettre dans la carte d’identité du cercle, uniquement
le cercle de centre O et de rayon 1, car j'ai veillé à écrire
des équations homogènes par rapport aux longueurs.
Dans les équations apparaissent donc en général
un facteur d’échelle, presque toujours appelé a, puis
des constantes appelées en général b, c
si ce sont des longueurs. Elles sont supposées non nulles et très
souvent positives.
La première équation est celle qui est la
plus classique, et non forcément l’équation cartésienne.
Suivent d’autres équations, et, dans le cas des courbes, un calcul
de l’abscisse curviligne et du rayon de courbure, éventuellement
des calculs de longueurs et d’aires.
Après l’encadré carte d’identité,
vient la définition la plus usitée de l’objet ; elle est
énoncée de façon générale, mais le lien
est fait avec le cas particulier (qui représente en fait la généralité)
de l’encadré. Lorsque j'emploie l’expression " ici ", je me réfère
à ce cas particulier.
Suivent alors d’autres caractérisations qui constituent
autant de propriétés de l’objet, et parfois d’autres propriétés
si elles sont classiques. Lorsque l’objet a été défini
moins pour lui-même que pour illustrer une propriété,
j'allège la partie équations et définitions pour insister
sur cette propriété.
J'ai enfin essayé de répertorier l'appartenance
de la forme aux diverses familles définies dans d'autres fiches,
et parfois découvert ainsi des liens inhabituels : les besaces
dans les courbes de Lissajous, les coniques dans les anticaustiques,
les courbes de Booth dans les
courbes de Watt par exemple !
Bonne lecture et vos commentaires,
encouragements et critiques sont les bienvenus !
 ,
tous deux fans d'ovales de Descartes, l'un en Suisse, l'autre aux États-Unis.
,
tous deux fans d'ovales de Descartes, l'un en Suisse, l'autre aux États-Unis.